题目内容
函数f（x）=
ax3+2ax2+x在R上单调递增，则实数a的取值范围为 ．
| 1 |
| 3 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，再分别讨论a的范围，从而解决问题．
解答：
解：∵函数f（x）=
ax3+2ax2+x，
∴f′（x）=ax2+4ax+1，
①a=0时，显然成立，
②a＞0时，令f′（x）=ax2+4ax+1=0，
∴△=4a（4a-1）≤0，
解得；0＜a≤
，
故答案为：[0，
]．
| 1 |
| 3 |
∴f′（x）=ax2+4ax+1，
①a=0时，显然成立，
②a＞0时，令f′（x）=ax2+4ax+1=0，
∴△=4a（4a-1）≤0，
解得；0＜a≤
| 1 |
| 4 |
故答案为：[0，
| 1 |
| 4 |
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
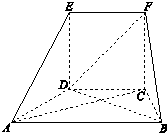在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AC=