题目内容
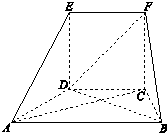 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=| 3 |
(Ⅰ)求证:AC⊥平面FBC;
(Ⅱ)线段AC上是否存在点M,使EA∥平面FDM?证明你的结论.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)利用勾股定理的逆定理即可得到AC⊥CB,又AC⊥FB,利用线面垂直的判定定理即可证明;
(Ⅱ)线段AC上存在点M,且M为AC中点时,有EA∥平面FDM.利用正方形的性质、三角形的中位线定理、线面平行的判定定理即可证明.
(Ⅱ)线段AC上存在点M,且M为AC中点时,有EA∥平面FDM.利用正方形的性质、三角形的中位线定理、线面平行的判定定理即可证明.
解答:
证明: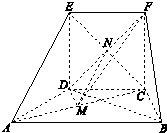 (Ⅰ)在△ABC中,
(Ⅰ)在△ABC中,
∵AC=
,AB=2,BC=1,∴AC2+BC2=AB2.
∴AC⊥BC.
又∵AC⊥FB,BF∩CB=B,
∴AC⊥平面FBC.
(Ⅱ)线段AC上存在点M,且M为AC中点时,有EA∥平面FDM,证明如下:
连接CE与DF交于点N,连接MN.
由 CDEF为正方形,得N为CE中点.
∴EA∥MN.
∵MN?平面FDM,EA?平面FDM,
∴EA∥平面FDM.
所以线段AC上存在点M,使得EA∥平面FDM成立.
 (Ⅰ)在△ABC中,
(Ⅰ)在△ABC中,∵AC=
| 3 |
∴AC⊥BC.
又∵AC⊥FB,BF∩CB=B,
∴AC⊥平面FBC.
(Ⅱ)线段AC上存在点M,且M为AC中点时,有EA∥平面FDM,证明如下:
连接CE与DF交于点N,连接MN.
由 CDEF为正方形,得N为CE中点.
∴EA∥MN.
∵MN?平面FDM,EA?平面FDM,
∴EA∥平面FDM.
所以线段AC上存在点M,使得EA∥平面FDM成立.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握勾股定理的逆定理、正方形的性质、三角形的中位线定理、线面平行的判定定理是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,D是边BC上一点,DC=2BD.
如图,在△ABC中,D是边BC上一点,DC=2BD.