题目内容
已知两直线l1:x+my+3=0,l2:(m-1)x+2my+2m=0,若l1∥l2,则m的值为( )
| A、0 | ||
B、-1或
| ||
| C、3 | ||
| D、0或3 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:给出的两直线方程均为一般式,直接由两直线平行和系数之间的关系列式求解m的值.
解答:
解:直线l1:x+my+3=0,l2:(m-1)x+2my+2m=0,
设A1=1,B1=m,C1=3,
A2=m-1,B2=2m,C2=2m,
∵l1∥l2,
∴
,即
,解得:m=0.
故选:A.
设A1=1,B1=m,C1=3,
A2=m-1,B2=2m,C2=2m,
∵l1∥l2,
∴
|
|
故选:A.
点评:本题考查直线的一般式方程与直线平行的关系,两直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0平行的充要条件是
,是基础题.
|

练习册系列答案
相关题目
已知两条直线l1:kx+(1-k)y-3=0和l2:(k-1)x+2y-2=0互相垂直,则k=( )
| A、1或-2 | B、-1或2 |
| C、1或2 | D、-1或-2 |
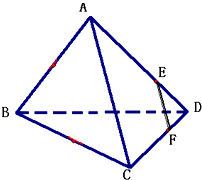 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明: