Question

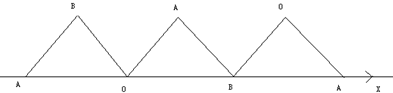
如图，在极坐标系Ox中，△OAB是正三角形，其中A（2，π），将△OAB沿极轴按顺时针方向滚动，点A从开始运动到第一次回到极轴上，其轨迹为G．

（1）求曲线G的极坐标方程；
（2）求曲线G与极轴所在直线围成的区域面积．

Answer 1

考点：简单曲线的极坐标方程,定积分

专题：坐标系和参数方程

分析：（1）直接由题意得到A由（2，π）转到（2，

π

3

）时的极坐标方程，然后求出A由（2，

π

3

）转到（4，0）时的直角坐标方程，结合公式ρ²=x²+y²，x=ρcosθ得答案；
（2）把曲线G与极轴所在直线围成的区域分割为两个半径是2，中心角是

2π

3

的扇形与一个边长为2的正三形，则区域面积可求．

解答： 解：（1）由题意可知，当A由（2，π）转到（2，

π

3

）时，极径为定值2；
当A由（2，

π

3

）转到（4，0）时，A点的轨迹是以（2，0）为圆心，以2为半径的圆弧，
圆弧的直角坐标方程为（x-2）²+y²=4（1≤x≤4）．
整理得，x²+y²=4x（1≤x≤4），
化为极坐标方程得：ρ=4cosθ(0≤θ≤

π

3

)．
∴曲线G的极坐标方程为ρ=

2， π 3 ＜θ≤π 4cosθ，0≤θ≤ π 3

；
（2）曲线G与极轴所在直线围成的区域可分为两个半径是2，中心角是

2π

3

的扇形与一个边长为2的正三角形，
面积等于2×

1

3

π×22+

1

2

×2×

3

=

8π

3

+

3

．

点评：本题考查了简单曲线的极坐标方程，考查了极坐标与直角坐标的互化，考查了圆的面积与三角形的面积公式，是中档题．