题目内容
“a=1”是“f(x)=
是奇函数”的( )
| a•2x-1 |
| 2x+a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据奇函数的定义,可得:若f(x)=
是奇函数,则a=1,或a=-1,进而根据充要条件的定义,可得答案.
| a•2x-1 |
| 2x+a |
解答:
解:若f(x)=
是奇函数,
则f(-x)=
=
=-f(x)=-
,
解得:a=1,或a=-1,
故“a=1”是“f(x)=
是奇函数”的充分不必要条件,
故选:A
| a•2x-1 |
| 2x+a |
则f(-x)=
| a•2-x-1 |
| 2-x+a |
| a-2x |
| 1+a•2x |
| a•2x-1 |
| 2x+a |
解得:a=1,或a=-1,
故“a=1”是“f(x)=
| a•2x-1 |
| 2x+a |
故选:A
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
已知等比数列{an}中,a1+a2=3,a2+a3=6,则a8=( )
| A、64 | B、128 |
| C、256 | D、512 |
若函数f(x)=
在x=1处可导,则实数a和b的值分别是( )
|
| A、1和0 | B、2和-1 |
| C、1和-2 | D、0和1 |
点A,B,C,D均在同一球面上,且AB、AC、AD两两垂直,且AB=1,AC=2,AD=3,则该球的表面积为( )
| A、7π | ||||
| B、14π | ||||
C、
| ||||
D、
|
如图是一个空间几何体的三视图,根据图中尺寸(单位:cm),可知该几何体的体积是( )

A、
| ||
B、3
| ||
C、6
| ||
D、18+2
|
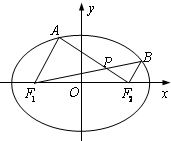 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆| x2 |
| 2 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
F为抛物线y2=2px (p>0)的焦点,过点F的直线与该抛物线交于A,B两点,l1,l2分别是该抛物线在A,B两点处的切线,l1,l2相交于点C,设|AF|=a,|BF|=b,则|CF|=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若f(x)=
,则f(x)的定义域为( )
| 1 | ||||
|
A、(-
| ||
| B、(-1,0) | ||
C、(-
| ||
| D、(0,+∞) |