题目内容
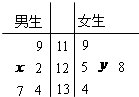 某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.
某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.(1)求x,y的值;
(2)现从成绩高于125分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(1)由已知中男生数据的中位数为125,可知120+x=125,由女生数据的平均数为126.8,可知126.8=
,解方程可得x,y的值;
(2)分别计算从成绩高于125分的同学中随机抽取两名同学的取法种数,和抽取的两名同学恰好为一男一女的取法种数,代入古典概型概率公式,可得答案.
| 119+125+120+y+128+134 |
| 5 |
(2)分别计算从成绩高于125分的同学中随机抽取两名同学的取法种数,和抽取的两名同学恰好为一男一女的取法种数,代入古典概型概率公式,可得答案.
解答:
解:(1)男生成绩为119,122,120+x,134,137,
其中位数为125,故x=5.…(3分)
女生成绩为119,125,120+y,128,134,
平均数为126.8=
,
解之得y=8…(6分)
(2)设成绩高于125的男生分别为a1、a2,
记a1=134,a2=137,
设成绩高于125的女生分别为b1、b2、b3,
记b1=128,b2=128,b3=134,
从高于12(5分)同学中取两人的所有取法:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),
(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3)共10种,…(8分)
其中恰好为一男一女的取法:
(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3)共6种,…(10分)
∵
=
故抽取的两名同学恰好为一男一女的概率为
.…(12分)
其中位数为125,故x=5.…(3分)
女生成绩为119,125,120+y,128,134,
平均数为126.8=
| 119+125+120+y+128+134 |
| 5 |
解之得y=8…(6分)
(2)设成绩高于125的男生分别为a1、a2,
记a1=134,a2=137,
设成绩高于125的女生分别为b1、b2、b3,
记b1=128,b2=128,b3=134,
从高于12(5分)同学中取两人的所有取法:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),
(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3)共10种,…(8分)
其中恰好为一男一女的取法:
(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3)共6种,…(10分)
∵
| 6 |
| 10 |
| 3 |
| 5 |
故抽取的两名同学恰好为一男一女的概率为
| 3 |
| 5 |
点评:此题考查了古典概型概率计算公式,茎叶图,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
相关题目
已知函数f(x)=x2-(k+1)2x+1,若存在x1∈[k,k+1],x2∈[k+2,k+4],使得f(x1)=f(x2),则实数k的取值范围为( )
A、[-
| ||||||||
B、[-
| ||||||||
| C、[-2,-1]∪[1,2] | ||||||||
D、[-
|
曲线f(x)=ex(其中e为自然对数的底数)在点(0,1)处的切线与直线y=-x+3和x轴所围成的区域D(包含边界),点P(x,y)为区域D内的动点,则z=x-3y的最大值为( )
| A、3 | B、4 | C、-1 | D、2 |
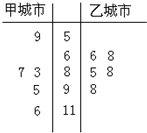 2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表:
2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表: