题目内容
已知实数k∈R,且k≠0,e为自然对数的底数,函数f(x)=
,g(x)=f(x)-x.
(1)如果函数g(x)在R上为减函数,求k的取值范围;
(2)如果k∈(0,4],求证:方程g(x)=0有且有一个根x=x0;且当x>x0时,有x>f(f(x))成立;
(3)定义:①对于闭区间[s,t],称差值t-s为区间[s,t]的长度;②对于函数g(x),如果对任意x1,x2∈[s,t]⊆D(D为函数g(x)的定义域),记h=|g(x2)-g(x1)|,h的最大值称为函数g(x)在区间[s,t]上的“身高”.问:如果k∈(0,4],函数g(x)在哪个长度为2的闭区间上“身高”最“矮”?
| k•ex |
| ex+1 |
(1)如果函数g(x)在R上为减函数,求k的取值范围;
(2)如果k∈(0,4],求证:方程g(x)=0有且有一个根x=x0;且当x>x0时,有x>f(f(x))成立;
(3)定义:①对于闭区间[s,t],称差值t-s为区间[s,t]的长度;②对于函数g(x),如果对任意x1,x2∈[s,t]⊆D(D为函数g(x)的定义域),记h=|g(x2)-g(x1)|,h的最大值称为函数g(x)在区间[s,t]上的“身高”.问:如果k∈(0,4],函数g(x)在哪个长度为2的闭区间上“身高”最“矮”?
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由函数g(x)在R上为减函数,可知g′(x)≤0,即k≤
,根据基本不等式求出
≥4,即可确定k的取值范围;
(2)由g(x)在R上为减函数,g(0)=
-0=
>0,g(4)<0,易得g(x)=0有且只有一个根x=x0.当x>x0时,有g(x)<g(x0)=0.即f(x)-x<0,从而x>f(x),又f(x)=
=
为增函数,f(x)>f(f(x)),所以x>f(f(x))成立;
(3)利用新定义得出x1,x2∈[t-2,t],且x1<x2时,h=|g(x2)-g(x1)|=2-k•
.当且仅当et=
,即t=1时,hmin=2-k•
.
从而函数g(x)在长度为2的闭区间[-1,1]上“身高”最“矮”.
| (ex+1)2 |
| ex |
| (ex+1)2 |
| ex |
(2)由g(x)在R上为减函数,g(0)=
| k |
| 1+1 |
| k |
| 2 |
| k•ex |
| ex+1 |
| k | ||
1+(
|
(3)利用新定义得出x1,x2∈[t-2,t],且x1<x2时,h=|g(x2)-g(x1)|=2-k•
| e-1 |
| e+1 |
| e2 |
| et |
| e-1 |
| e+1 |
从而函数g(x)在长度为2的闭区间[-1,1]上“身高”最“矮”.
解答:
解:(1)∵g(x)=f(x)-x=
-x在R上为减函数,
∴g′(x)=
-1=
-1≤0恒成立.
即k≤
恒成立.
∵
=ex+
+2≥2+2=4.
当且仅当ex=
,即x=0时,
的最小值为4.
又由k≠0,
∴k的取值范围为(-∞,0)∪(0,4].
(2)由(1)知,
k∈(0,4]时,g(x)在R上为减函数.
又g(0)=
-0=
>0,
g(4)=
-4=
=
,
∵k≤4,
∴(k-4)e4-4<0,
∴g(4)<0.
∴g(x)=0在(0,4)上有一个根x=x0.
又g(x)在R上为减函数,
∴g(x)=0有且只有一个根x=x0.
∴当x>x0时,有g(x)<g(x0)=0.
即f(x)-x<0,
∴x>f(x).①
又∵f(x)=
=
为增函数,
∴f(x)>f(f(x))②.
由①②得,x>f(f(x))成立.
(3)设x1,x2∈[t-2,t],且x1<x2,
由(1)知,k∈(0,4]时g(x)在R上为减函数,
∴h=|g(x2)-g(x1)|=g(x1)-g(x2)
≤g(t-2)-g(t)
=[f(t-2)-t-2]-[f(t)-t]
=f(t-2)-f(t)+2
=
-
+2
=k[
-
]+2
=k•et•
+2
=2-
≥2-
=2-k•
.
其中k(e2-1)>0,当且仅当et=
,即t=1时,hmin=2-k•
.
∴函数g(x)在长度为2的闭区间[-1,1]上“身高”最“矮”.
| k•ex |
| ex+1 |
∴g′(x)=
| kex(ex+1)-kex•ex |
| (ex+1)2 |
| kex |
| (ex+1)2 |
即k≤
| (ex+1)2 |
| ex |
∵
| (ex+1)2 |
| ex |
| 1 |
| ex |
当且仅当ex=
| 1 |
| ex |
| (ex+1)2 |
| ex |
又由k≠0,
∴k的取值范围为(-∞,0)∪(0,4].
(2)由(1)知,
k∈(0,4]时,g(x)在R上为减函数.
又g(0)=
| k |
| 1+1 |
| k |
| 2 |
g(4)=
| k•e4 |
| e4+1 |
| ke4-4e4-4 |
| e4+1 |
| (k-4)e4-4 |
| e4+1 |
∵k≤4,
∴(k-4)e4-4<0,
∴g(4)<0.
∴g(x)=0在(0,4)上有一个根x=x0.
又g(x)在R上为减函数,
∴g(x)=0有且只有一个根x=x0.
∴当x>x0时,有g(x)<g(x0)=0.
即f(x)-x<0,
∴x>f(x).①
又∵f(x)=
| k•ex |
| ex+1 |
| k | ||
1+(
|
∴f(x)>f(f(x))②.
由①②得,x>f(f(x))成立.
(3)设x1,x2∈[t-2,t],且x1<x2,
由(1)知,k∈(0,4]时g(x)在R上为减函数,
∴h=|g(x2)-g(x1)|=g(x1)-g(x2)
≤g(t-2)-g(t)
=[f(t-2)-t-2]-[f(t)-t]
=f(t-2)-f(t)+2
=
| k•et-2 |
| et-2+1 |
| k•et |
| et+1 |
=k[
| et |
| et+e2 |
| et |
| et+1 |
=k•et•
| 1-e2 |
| (et+e2)(et+1) |
=2-
| k(e2-1) | ||
et+
|
≥2-
| k(e2-1) | ||||
2
|
=2-k•
| e-1 |
| e+1 |
其中k(e2-1)>0,当且仅当et=
| e2 |
| et |
| e-1 |
| e+1 |
∴函数g(x)在长度为2的闭区间[-1,1]上“身高”最“矮”.
点评:本题考查导数在研究函数单调性中的应用,基本不等式以及新定义问题的处理技巧和基本运算能力,属于难题.

练习册系列答案
相关题目
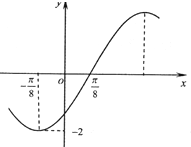 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<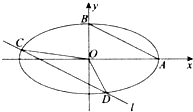 如图,A、B是椭圆
如图,A、B是椭圆