题目内容
把曲线ysinx-2y+3=0先沿x轴向左平移
个单位长度,再沿y轴向下平移1个单位长度,得到曲线方程是( )
| π |
| 2 |
| A、(1-y)cosx+2y-3=0 |
| B、(1+y)sinx-2y+1=0 |
| C、(1+y)cosx-2y+1=0 |
| D、-(1+y)cosx+2y+1=0 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:把曲线ysinx-2y+3=0先沿x轴向左平移
个单位长度,可得曲线ysin(x+
)-2y+3=0,再沿y轴向下平移1个单位长度,可得曲线(y+1)sin(x+
)-2(y+1)+3=0,整理可得答案.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:
解:把曲线ysinx-2y+3=0先沿x轴向左平移
个单位长度,
可得曲线ysin(x+
)-2y+3=0,
再沿y轴向下平移1个单位长度,
可得曲线(y+1)sin(x+
)-2(y+1)+3=0,
即曲线(1+y)cosx-2y+1=0,
故选:C.
| π |
| 2 |
可得曲线ysin(x+
| π |
| 2 |
再沿y轴向下平移1个单位长度,
可得曲线(y+1)sin(x+
| π |
| 2 |
即曲线(1+y)cosx-2y+1=0,
故选:C.
点评:本题考查的知识点是平面移图与移轴,熟练掌握曲线平移的原则,f(x,y)=0向左平移a个单位,再向下平移b个单位,得到f(x+a,y+b)=0,是解答的关键.

练习册系列答案
相关题目
设a=
,b=
,c=
,则a,b,c的大小关系是( )
| 4 | 24 |
| 3 | 12 |
| 6 |
| A、a>b>c |
| B、b<c<a |
| C、b>c>a |
| D、a<b<c |
若抛物线y2=2px的焦点与椭圆
+
=1的右焦点重合,则p的值为( )
| x2 |
| 6 |
| y2 |
| 2 |
| A、-2 | B、2 | C、-4 | D、4 |
不等式(x+y-2)(x-y+1)≥0表示的平面区域时( )
A、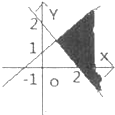 |
B、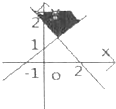 |
C、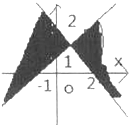 |
D、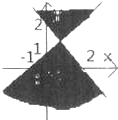 |