题目内容
 在如图所示的多面体中,四边形ABCD是梯形,∠BAD=∠CDA=90°,四边形CDEF是矩形,平面ABCD⊥平面CDEF,AB=AD=DE=
在如图所示的多面体中,四边形ABCD是梯形,∠BAD=∠CDA=90°,四边形CDEF是矩形,平面ABCD⊥平面CDEF,AB=AD=DE=| 1 |
| 2 |
(I)求证:AC∥平面MDF;
(Ⅱ)平面MDF将该几何体分成两部分,求多面体MDFE和多面体ABCDMF的体积之比.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(I)证连结CE,交DE于N,连结MN,由此得MN∥AC,由此能求出AC∥平面MDF.
(II)将多面体ABCDEF补成三棱柱ADE-B'CF,由此能求三棱柱的体积,V多面体ABCDEF=V三棱柱ADE-BCF-VF-BB′C,三棱锥F-DEM的体积VM-DEF=
,由此能求出多面体MDFE和多面体ABCDMF的体积之比.
(II)将多面体ABCDEF补成三棱柱ADE-B'CF,由此能求三棱柱的体积,V多面体ABCDEF=V三棱柱ADE-BCF-VF-BB′C,三棱锥F-DEM的体积VM-DEF=
| 4 |
| 3 |
解答:
(I)证明:连结CE,交DE于N,连结MN,
由题意知N为CE的中点,
在△ACE中,MN∥AC,…(3分)
且MN?面MDF,AC?平面MDF,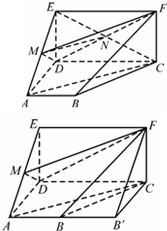
∴AC∥平面MDF.…(6分)
(II) 解:将多面体ABCDEF补成三棱柱ADE-B'CF,如图,
则三棱柱的体积为:
V=S△ADE•CD=
×2×2×4=8,…(8分)
则V多面体ABCDEF=V三棱柱ADE-BCF-VF-BB′C
=8-
=
.…(10分)
而三棱锥F-DEM的体积VM-DEF=
,
∴多面体MDFE和多面体ABCDMF的体积之比为
=
.…(12分)
由题意知N为CE的中点,
在△ACE中,MN∥AC,…(3分)
且MN?面MDF,AC?平面MDF,

∴AC∥平面MDF.…(6分)
(II) 解:将多面体ABCDEF补成三棱柱ADE-B'CF,如图,
则三棱柱的体积为:
V=S△ADE•CD=
| 1 |
| 2 |
则V多面体ABCDEF=V三棱柱ADE-BCF-VF-BB′C
=8-
| 4 |
| 3 |
| 20 |
| 3 |
而三棱锥F-DEM的体积VM-DEF=
| 4 |
| 3 |
∴多面体MDFE和多面体ABCDMF的体积之比为
| VM-DEF |
| VABCDEF |
| 1 |
| 5 |
点评:本题考查直线与平面平行的证明,考查多面体MDFE和多面体ABCDMF的体积之比的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=(λ,2),
=(-3,5),且
与
的夹角为锐角,则λ的取值范围( )
| a |
| b |
| a |
| b |
A、λ<
| ||||
B、λ≥
| ||||
C、λ<
| ||||
D、λ≤
|
已知sinx=
,则cos2x的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=(
)x-1的定义域、值域分别是( )
| 1 |
| 2 |
| A、定义域是R,值域是R |
| B、定义域是R,值域是(0,+∞) |
| C、定义域是(0,+∞),值域是R |
| D、定义域是R,值域是(-1,+∞) |
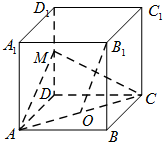 在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.
在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.