题目内容

M，N分别是四面体OABC的边OA，BC的中点，P，Q是MN的三等分点，用向量
OA
，
OB
，
OC
表示
OP
和
OQ
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：先根据向量的加法及减法用向量
OA
，
OB
，
OC
表示出
MN
：
MN
=-
1
2
OA
+
1
2
OB
+
1
2
OC
，而
OP
=
1
2
OA
+
1
3
MN
，
OQ
=
1
2
OA
+
2
3
MN
，所以带入
MN
即可完成解答．
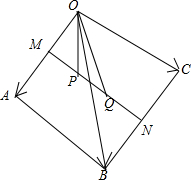解答： 解：如图，
MN
=
MO
+
OC
+
CN
=-
1
2
OA
+
OC
+
1
2
CB
=-
1
2
OA
+
1
2
OC
+
1
2
(
OB
-
OC
)=-
1
2
OA
+
1
2
OB
+
1
2
OC
；
∴
OP
=
OM
+
MP
=
1
2
OA
+
1
3
MN
=
1
2
OA
+
1
3
•(-
1
2
OA
+
1
2
OB
+
1
2
OC
)=
1
3
OA
+
1
6
OB
+
1
6
OC
；
OQ
=
1
2
OA
+
2
3
MN
=
1
2
OA
+
2
3
•(-
1
2
OA
+
1
2
OB
+
1
2
OC
)=
1
6
OA
+
1
3
OB
+
1
3
OC
．
点评：考查向量的加法、减法运算，以及共线向量基本定理．
练习册系列答案
相关题目
已知抛物线y2=4x的焦点为F，过点F作一条直线l与抛物线交于A（x1，y1），B（x2，y2）两点
（Ⅰ）求以点F为圆心，且与直线y=x相切的圆的方程
（Ⅱ）从x1，x2，|y1|，|y2|，1，2中取出三个量，使其构成等比数列，并予以证明．
已知数列{an}的前n项和Sn=
1
4
an+
3
4
，则{an}的通项公式an=
 
．
已知极坐标系的极点在直角坐标系的原点处，极轴与x轴的正半轴重合，直线l的极坐标方程为：ρsin(θ-
π
6
)=
1
2
，曲线C的参数方程为：
x=2+2cosα
y=2sinα
（α为参数）．
（I）写出直线l的直角坐标方程；
（Ⅱ）求曲线C上的点到直线l的距离的最大值．
命题：p：?x∈R，x2+1＞a，命题q：
x2
a2
+
y2
4
=1是焦点在x轴上的椭圆，若p∧q为真，p∧q为假，求实数a的取值范围．
10件产品中有8件正品，2件次品，从中任取3件，则恰好有一件次品的概率为
 
．（结果用最简分数表示）
执行如图所示的程序框图，若输入n的值为8，则输出Sn=
n(12+12n)
2
=6n2+6n的值为（　　）
A、4B、8C、10D、12
在如图所示的多面体中，四边形ABCD是梯形，∠BAD=∠CDA=90°，四边形CDEF是矩形，平面ABCD⊥平面CDEF，AB=AD=DE=
1
2
CD=2，M是线段AE的中点．
（I）求证：AC∥平面MDF；
（Ⅱ）平面MDF将该几何体分成两部分，求多面体MDFE和多面体ABCDMF的体积之比．
已知cosα=
3
5
，cosβ=
5
5
，其中α，β都是锐角．求：
（I）sin（α-β）的值； 
（Ⅱ）tan（α+β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网