题目内容
9.四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=3,AB=2,BC=$\sqrt{3}$,求P到BD的距离.
分析 过A作AE⊥BD,垂足为E,连接PE,则PE为点P到对角线BD的距离,即可得出结论.
解答 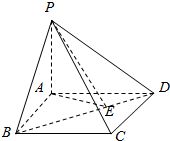 解:如图所示,过A作AE⊥BD,垂足为E,连接PE
解:如图所示,过A作AE⊥BD,垂足为E,连接PE
则PE为点P到对角线BD的距离
∵矩形ABCD,AB=2,BC=$\sqrt{3}$,可得BD=$\sqrt{7}$,
∴2×$\sqrt{3}$=$\sqrt{7}$×AE
∴AE=$\frac{2\sqrt{21}}{7}$,
又∵PA=3,PA⊥矩形ABCD
∴PE=$\sqrt{{(\frac{2\sqrt{21}}{7})}^{2}+{{3}^{2}}^{\;}}$=$\frac{5\sqrt{21}}{7}$.
故答案为:$\frac{5\sqrt{21}}{7}$.
点评 本题考查空间距离,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
19.已知向量$\overrightarrow{a}$=($\frac{1}{2}$,k),$\overrightarrow{b}$=(k-1,4),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数k的值为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | -$\frac{1}{7}$ | D. | 2 |
20.李华经营了两家电动轿车销售连锁店,其月利润(单位:元)分别为L1=-5x2+900x-10000,L2=300x-1000(其中x为销售辆数),若某月两连锁店共销售了110辆,则能获得的最大利润为( )
| A. | 11000 | B. | 22000 | C. | 33000 | D. | 40000 |
4.复数z=$\frac{2}{1-i}$,则复数z的模是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
1.某几何体的三视图如图所示,则该几何体的体积是( )
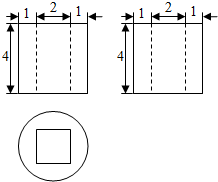

| A. | 16π-16 | B. | 16π | C. | 16π-8 | D. | 64 |