题目内容
4.复数z=$\frac{2}{1-i}$,则复数z的模是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 直接由复数代数形式的乘除运算化简复数z,则复数z的模可求.
解答 解:由复数z=$\frac{2×(1+i)}{(1-i)(1+i)}=1+i$,
则|z|=$\sqrt{1+1}=\sqrt{2}$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
15.若集合A={x|$\sqrt{x}$>2},B={x|1<x<5},则A∩B等于( )
| A. | (1,4) | B. | (4,5) | C. | (1,5) | D. | (5,+∞) |
19.设Sn为等差数列{an}的前n项和,若a3=3,S9-S6=27,则该数列的首项a1等于( )
| A. | $-\frac{6}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
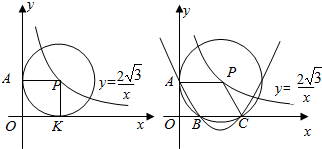 在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
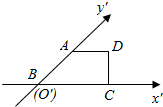 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.