题目内容
已知命题p:不等式(a-2)x2+2(a-2)x-4<0,对?x∈R恒成立;命题q:关于x的方程x2+(a-1)x+1=0的一个根在(0,1)上,另一个根在(1,2)上,若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先根据二次函数的最大值及二次函数的图象求出命题p,q下a的取值范围,再根据p∨q为真命题,p∧q为假命题得到p真q假,和p假q真两种情况,求出每种情况下a的取值范围再求并集即可.
解答:
解:由命题p知,函数(a-2)x2+2(a-2)x-4的最大值小于0;
a=2时,-4<0,∴符合题意;
a≠2时,则a需满足:
,解得-2<a<2;
∴命题p:-2<a≤2;
根据命题q,设f(x)=x2+(a-1)x+1,所以:
,解得-
<a<-1;
∴命题q:-
<a<-1;
若p∨q为真命题,p∧q为假命题,则p,q一真一假:
p真q假时,
,∴-2<a≤-
,或-1≤a≤2;
p假q真时,
,∴a∈∅;
∴实数a的取值范围为(-2,-
]∪[-1,2].
a=2时,-4<0,∴符合题意;
a≠2时,则a需满足:
|
∴命题p:-2<a≤2;
根据命题q,设f(x)=x2+(a-1)x+1,所以:
|
| 3 |
| 2 |
∴命题q:-
| 3 |
| 2 |
若p∨q为真命题,p∧q为假命题,则p,q一真一假:
p真q假时,
|
| 3 |
| 2 |
p假q真时,
|
∴实数a的取值范围为(-2,-
| 3 |
| 2 |
点评:考查二次函数的最大值的计算公式,注意讨论二次项的系数是否为0的情况,注意结合二次函数图象,以及p∨q,p∧q真假和p,q真假的关系.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在△ABC中,a=1,b=
,∠A=
,则∠B等于( )
| 3 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=
在[2,+∞)上( )
| 1 |
| x |
| A、有最大值无最小值 |
| B、有最小值无最大值 |
| C、有最大值和最小值 |
| D、无最大值和最小值 |
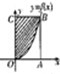 如图,长方形四个顶点为O(0,0),A(
如图,长方形四个顶点为O(0,0),A(