Question

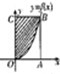如图，长方形四个顶点为O（0，0），A（

2

，0），B（

2

，2

2

），C（0，2

2

），若幂函数y=f（x）图象经过点B，则图中阴影部分的面积为

 

．

Answer 1

考点：定积分在求面积中的应用

专题：导数的综合应用

分析：首先利用待定系数法求幂函数的解析式，然后求出矩形面积，利用定积分求出曲线与x轴、x=

2

围成的面积，阴影部分的面积等于矩形面积减去定积分．

解答： 解：设幂函数解析式为y=x^a，∵曲线经过点B（

2

，2

2

），
∴a=3，y=x³，
∴长方形部分面积S=

2

×2

2

=4，
阴影部分面积S_阴影=4-

∫

2 0

x3dx=4-

1

4

x⁴|

2 0

=3；
故答案为：3．

点评：本题考查了待定系数法求解析式以及定积分求曲边梯形的面积，经常考查注意熟练掌握．