题目内容
已知两直线x-ky-k=0与y=k（x-1）平行，则k的值为 ．
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：由平行关系可得直线斜率相等，解k值验证排除重合即可．
解答：
解：由方程可知y=k（x-1）的斜率为k，
由平行关系可得直线x-ky-k=0的斜率
=k，
解得k=1或k=-1，
经验证当k=1时，两直线重合，
当k=-1时，两直线平行，
故答案为：-1
由平行关系可得直线x-ky-k=0的斜率
| 1 |
| k |
解得k=1或k=-1，
经验证当k=1时，两直线重合，
当k=-1时，两直线平行，
故答案为：-1
点评：本题考查直线的一般式方程与平行关系，属基础题．
练习册系列答案
相关题目
已知命题p：f（x）=
e-x在（0，+∞）上单调递减；命题q：双曲线
-
=1的焦点到抛物线x2=
y的准线的距离为2，则下列命题正确的是（ ）
| 1 | ||
|
| x2 |
| 4 |
| y2 |
| 5 |
| 1 |
| 4 |
| A、p∨q | B、p∧q |
| C、￢p∧q | D、￢p∨q |
如图是某几何体的三视图，它的正视图和侧视图均为矩形，俯视图为正三角形（长度单位：cm）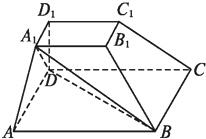
如图，在四棱台ABCD-A1B1C1D1中，D1D⊥平面ABCD，底面ABCD是平行四边形，AB=2A1B1=2AD=2DD1，∠BAD=60°．