题目内容
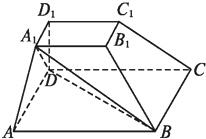 如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.(Ⅰ)证明:AA1⊥BD;
(Ⅱ)求A1B与面A1ADD1成角的余弦值;
(Ⅲ)证明:直线CC1∥平面A1BD.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ) 由D1D⊥平面ABCD,可证 D1D⊥BD.△ABD 中,由余弦定理得 BD2,勾股定理可得 AD⊥BD,由线面垂直的判定定理可证 BD⊥面ADD1A1,再由线面垂直的性质定理可证 BD⊥AA1;
(Ⅱ)BD⊥面ADD1A1,∴∠BA1D即A1B与面A1ADD1成的角,在Rt△BA1D中计算;
(Ⅲ)连接AC和A1C1,设AC∩BD=E,先证明四边形ECC1A1为平行四边形,可得CC1∥A1E,再由线面平行的判定定理可证CC1∥平面A1BD.
(Ⅱ)BD⊥面ADD1A1,∴∠BA1D即A1B与面A1ADD1成的角,在Rt△BA1D中计算;
(Ⅲ)连接AC和A1C1,设AC∩BD=E,先证明四边形ECC1A1为平行四边形,可得CC1∥A1E,再由线面平行的判定定理可证CC1∥平面A1BD.
解答:
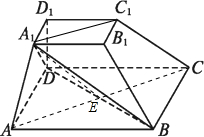 证明:(Ⅰ)∵D1D⊥平面ABCD,
证明:(Ⅰ)∵D1D⊥平面ABCD,
∴D1D⊥BD.
又AB=2AD,AD=A1B1,∠BAD=60°,
△ABD 中,由余弦定理得
BD2=AD2+AB2-2AB•ADcos60°=3AD2,
∴AD2+BD2=AB2,
∴AD⊥BD,又 AD∩DD1=D,∴BD⊥面ADD1A1.
由 AA1?面ADD1A1,
∴BD⊥AA1.
(Ⅱ)解:由(Ⅰ)知,BD⊥面ADD1A1,
∴∠BA1D即A1B与面A1ADD1成的角,设AB=2,A1B1=AD=DD1=1,
由棱台的定义,A1D1=
,D1D⊥平面ABCD,
∴D1D⊥面A1B1C1D1,Rt△DD1A1,A1D=
,
在Rt△ABD中,BD=
,在Rt△BA1D中,A1B=
,
∴cos∠BA1D=
=
;
(Ⅲ)证明:连接AC 和A1C1,设 AC∩BD=E,
由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1 A1 为平行四边形,
∴CC1∥A1 E,而A1 E?平面A1BD,∴CC1∥平面A1BD.
 证明:(Ⅰ)∵D1D⊥平面ABCD,
证明:(Ⅰ)∵D1D⊥平面ABCD,∴D1D⊥BD.
又AB=2AD,AD=A1B1,∠BAD=60°,
△ABD 中,由余弦定理得
BD2=AD2+AB2-2AB•ADcos60°=3AD2,
∴AD2+BD2=AB2,
∴AD⊥BD,又 AD∩DD1=D,∴BD⊥面ADD1A1.
由 AA1?面ADD1A1,
∴BD⊥AA1.
(Ⅱ)解:由(Ⅰ)知,BD⊥面ADD1A1,
∴∠BA1D即A1B与面A1ADD1成的角,设AB=2,A1B1=AD=DD1=1,
由棱台的定义,A1D1=
| 1 |
| 2 |
∴D1D⊥面A1B1C1D1,Rt△DD1A1,A1D=
| ||
| 2 |
在Rt△ABD中,BD=
| 3 |
| ||
| 2 |
∴cos∠BA1D=
| A1D |
| A1B |
| ||
| 17 |
(Ⅲ)证明:连接AC 和A1C1,设 AC∩BD=E,
由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1 A1 为平行四边形,
∴CC1∥A1 E,而A1 E?平面A1BD,∴CC1∥平面A1BD.
点评:本题考查余弦定理、勾股定理、线面角的计算、线面平行的判定定理、线面平行的性质定理的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
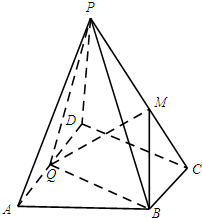 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC=