题目内容
不等式|x-4|+|x-3|>a对一切实数x恒成立,实数a的取值范围 .
考点:绝对值不等式的解法
专题:计算题,不等式
分析:令g(x)=|x-4|+|x-3|,利用绝对值不等式可求得g(x)min,从而可求得实数a的取值范围.
解答:
解:g(x)=|x-4|+|x-3|,
则g(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,
∴g(x)min=1.
∵不等式|x-4|+|x-3|>a,对一切实数x都成立,
∴a<g(x)min=1.
∴实数a的取值范围是(-∞,1).
故答案为:(-∞,1).
则g(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,
∴g(x)min=1.
∵不等式|x-4|+|x-3|>a,对一切实数x都成立,
∴a<g(x)min=1.
∴实数a的取值范围是(-∞,1).
故答案为:(-∞,1).
点评:本题考查绝对值不等式,求得g(x)min是关键,考查构造函数思想与转化、运算能力,属于中档题.

练习册系列答案
相关题目
已知首项为正数的等差数列{an}的前n项和为Sn,若a1006,a1007是方程x2-2012x-2011=0的两根,则使Sn>0成立的正整数n的最大值是( )
| A、1006 | B、1007 |
| C、2011 | D、2012 |
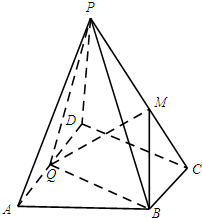 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC=