题目内容
6.已知数列{an}的前n项和为Sn,且n+1=1+Sn对一切正整数n恒成立.(1)试求当a1为何值时,数列{an}是等比数列,并求出它的通项公式;
(2)在(1)的条件下,当n为何值时,数列$\left\{{lg\frac{400}{a_n}}\right\}$的前n项和Tn取得最大值.
分析 (1)由已知数列递推式可得an+1=2an,再由数列{an}是等比数列求得首项,并求出数列通项公式;
(2)把数列{an}的通项公式代入数列$\left\{{lg\frac{400}{a_n}}\right\}$,可得数列$\left\{{lg\frac{400}{a_n}}\right\}$是递减数列,可知当n=9时,数列$\left\{{lg\frac{400}{a_n}}\right\}$的项为正数,n=10时,数列$\left\{{lg\frac{400}{a_n}}\right\}$的项为负数,则答案可求.
解答 解:(1)由an+1=1+Sn得:当n≥2时,an=1+Sn-1,
两式相减得:an+1=2an,
∵数列{an}是等比数列,∴a2=2a1,
又∵a2=1+S1=1+a1,解得:a1=1.
得:${a_n}={2^{n-1}}$;
(2)$lg\frac{400}{{a}_{n}}=lg\frac{400}{{2}^{n-1}}$,可知数列$\{lg\frac{400}{{{2^{n-1}}}}\}$是一个递减数列,
∴$lg\frac{400}{2^0}>lg\frac{400}{2^1}>lg\frac{400}{2^2}>…>lg\frac{400}{2^8}>0>lg\frac{400}{2^9}>…$,
由此可知当n=9时,数列$\left\{{lg\frac{400}{a_n}}\right\}$的前项和Tn取最大值.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,考查数列的函数特性,是中档题.

练习册系列答案
相关题目
14.已知函数$f(x)=\sqrt{3}sin2x-cos2x$的图象在区间$[{0,\frac{a}{3}}]$和$[{2a,\frac{4π}{3}}]$上均单调递增,则正数a的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{12}}]$ | B. | $[{\frac{5π}{12},π}]$ | C. | $[{\frac{π}{4},π}]$ | D. | $[{\frac{π}{4},\frac{2π}{3}}]$ |
1.上饶高铁站B1进站口有3个闸机检票通道口,若某一家庭有3个人检票进站,如果同一个人进的闸机检票通道口选法不同,或几个人进同一个闸机检票通道口但次序不同,都视为不同的进站方式,那么这个家庭3个人的不同进站方式有( )种.
| A. | 24 | B. | 36 | C. | 42 | D. | 60 |
11.已知集合M={x|1<x≤3},若N={x|2<x≤5},则M∪N=( )
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
18.已知实数x,y满足不等式组$\left\{\begin{array}{l}{-3≤3x-y≤-1}\\{-1≤x+y≤1}\end{array}\right.$,若z=ax+y有最大值$\frac{5}{2}$,则实数a的值是( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
15.执行如图的程序框图,则输出的结果为( )
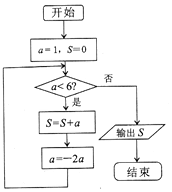

| A. | 15 | B. | 3 | C. | -11 | D. | -5 |