题目内容
9.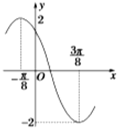 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,(1)求函数的解析式;
(2)求这个函数的单调递增区间.
分析 (1)由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)利用正弦函数的单调性,求得这个函数的单调递增区间.
解答 解:(1)由图可知:A=2,$\frac{T}{2}=\frac{3π}{8}-(-\frac{π}{8})=\frac{π}{2}$,所以T=π,由$T=\frac{2π}{ω}$得ω=2,
所以y=2sin(2x+ϕ),又因为该图象过点$(-\frac{π}{8},2)$,
所以$2=2sin[2×(-\frac{π}{8})+ϕ]$,即$sin(-\frac{π}{4}+ϕ)=1$,
所以$-\frac{π}{4}+ϕ=\frac{π}{2}+2kπ,k∈Z$即$ϕ=\frac{3π}{4}+2kπ,k∈Z$,
又因为|ϕ|<π,所以$ϕ=\frac{3π}{4}$,∴函数y=2sin(2x+$\frac{3π}{4}$).
(2)由$-\frac{π}{2}+2kπ≤2x+\frac{3π}{4}≤\frac{π}{2}+2kπ,k∈Z$,
得$-\frac{5π}{4}+2kπ≤2x≤-\frac{π}{4}+2kπ,k∈Z$,即$-\frac{5π}{8}+kπ≤x≤-\frac{π}{8}+kπ,k∈Z$,
所以这个函数的单调增区间为$[-\frac{5π}{8}+kπ,-\frac{π}{8}+kπ](k∈Z)$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,正弦函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.式子$\frac{1}{{2-{{cos}^2}θ}}$+$\frac{1}{{2-{{sin}^2}θ}}$(θ∈R)的最小值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )
| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
19.设随机变量X服从正态分布N(2,22),则P(2<X<3)可以表示为( )
| A. | 1~P(X<1) | B. | $\frac{1-2P(X<1)}{2}$ | C. | P(0<X<1) | D. | $\frac{1+2P(X<1)}{2}$ |


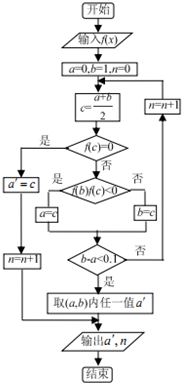 如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )
如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )