题目内容
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
分析 根据三角形相似求出交线所在圆的半径即可.
解答 解: 设球与圆柱母线SB交于C,过C作CD⊥SO,则球的表面与该圆锥的表面的交线为以CD为半径的圆周.
设球与圆柱母线SB交于C,过C作CD⊥SO,则球的表面与该圆锥的表面的交线为以CD为半径的圆周.
∵△SDC∽△SOB,
∴$\frac{CD}{OB}=\frac{SC}{SB}$,即$\frac{CD}{\sqrt{3}}=\frac{\sqrt{3}}{2}$,解得CD=$\frac{3}{2}$.
∴球的表面与该圆锥的表面的交线长为2π×$\frac{3}{2}$=3π.
故选A.
点评 本题考查了圆锥与球的结构特征,属于基础题.

练习册系列答案
相关题目
8.复数$\frac{-i}{3+i}$在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
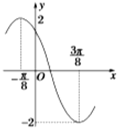 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示, 如图,已知平行于圆柱轴的截面ABB1A1是正方形,面积为3a2,它与轴的距离是底面半径的一半,求圆柱的全面积和体积.
如图,已知平行于圆柱轴的截面ABB1A1是正方形,面积为3a2,它与轴的距离是底面半径的一半,求圆柱的全面积和体积.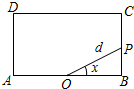 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中: