题目内容
19.设随机变量X服从正态分布N(2,22),则P(2<X<3)可以表示为( )| A. | 1~P(X<1) | B. | $\frac{1-2P(X<1)}{2}$ | C. | P(0<X<1) | D. | $\frac{1+2P(X<1)}{2}$ |
分析 利用正态分布的对称性,即可得出结论.
解答 解:∵随机变量X服从正态分布X~N(2,22),
∴μ=2,?=2,
∴P(2<X<3)=P(1<X<2)=$\frac{1-2P(X<1)}{2}$.
故选:B.
点评 本题考查概率的计算,考查正态分布,比较基础.

练习册系列答案
相关题目
7.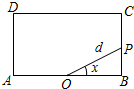 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
①f(x)有最小值1;
②f(x)有最大值$\sqrt{2}$;
③f(x)有3个极值点;
④f(x)有4个单调区间.
其中正确的是( )
 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:①f(x)有最小值1;
②f(x)有最大值$\sqrt{2}$;
③f(x)有3个极值点;
④f(x)有4个单调区间.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ①②④ | D. | ①②③④ |
4.已知等差数列{an}的前n项和为Sn,a2=-2,a8=6,则S9=( )
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
11.方程组$\left\{\begin{array}{l}{ax-y=0}\\{x-(2a-1)y=1}\end{array}\right.$有且只有一个解,则a的取值范围为( )
| A. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞) | B. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,+∞) | ||
| C. | (-∞,1)∪(1,+∞) | D. | R |
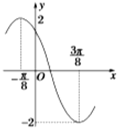 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,