题目内容
17．若x＞0，则$4x+\frac{1}{x}$的最小值为4．分析 因为x＞0，直接利用基本不等式求出其最小值．
解答 解：若x＞0，则4x+$\frac{1}{x}$≥2$\sqrt{4x•\frac{1}{x}}$=4，
当且仅当4x=$\frac{1}{x}$，x=$\frac{1}{2}$时取得．
故答案为：4．
点评 本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，属于基础题．
练习册系列答案
相关题目
7．设x，y∈R，a＞1，b＞1，若ax=by=3，a+2b=6$\sqrt{2}$，则$\frac{1}{x}$+$\frac{1}{y}$的最大值是（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
8．复数$\frac{-i}{3+i}$在复平面上对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
12．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | 1 |
2．要得到函数y=2sin（2x+$\frac{2π}{3}$）的图象，需要将函数y=2sin2x的图象（ ）
| A． | 向左平移$\frac{2π}{3}$个单位 | B． | 向右平移$\frac{2π}{3}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
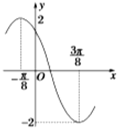已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示，
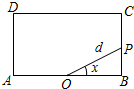如图，已知矩形ABCD中，AB=2，BC=1，O为线段AB的中点，动点P从B出发，沿矩形ABCD的边逆时针运动，运动至A点时终止．设∠BOP=x，OP=d，将d表示为x的函数d=f（x）．则下列命题中：