题目内容
20.已知数列{an}是各项均不为零的等差数列,Sn为其前n项和,且an=$\sqrt{{S}_{2n-1}}$(n∈N*),A=-a1a2+a2a3-a3a4+a4a5-…+a2na2n+1,则A=8n2+4n.分析 由已知条件利用等差数列的性质求出a1=1,d=2,从而得到an=2n-1,由此能求出A=-a1a2+a2a3-a3a4+a4a5-…+a2na2n+1的值.
解答 解:∵数列{an}是各项均不为零的等差数列,Sn为其前n项和,且an=$\sqrt{{S}_{2n-1}}$(n∈N*),
∴${{a}_{n}}^{2}$=S2n-1,
分别令n=1,n=2,
得$\left\{\begin{array}{l}{{{a}_{1}}^{2}={S}_{1}={a}_{1}}\\{{{a}_{2}}^{2}=({a}_{1}+d)^{2}=3{a}_{1}+3d}\end{array}\right.$,
解得a1=1,d=2,
∴an=2n-1,
∴A=-a1a2+a2a3-a3a4+a4a5-…+a2na2n+1
a2(a3-a1)+a4(a5-a3)+…+a2n(a2n+1-a2n-1)
=4(a2+a4+…+a2n)
=$4×\frac{n(3+4n-1)}{2}$
=8n2+4n.
故答案为:8n2+4n.
点评 本题考查等差数列的若干项和的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
11.在某中学高一年级的160名学生中开展一项社会调查,先将学生随机编号为1,2,3,…,159,160,采用系统抽样的方法(等间距地抽取,每段抽取一个个体).已知抽取的学生中最小的两个编号为6,22,那么抽取的学生中,最大的编号应该是( )
| A. | 141 | B. | 142 | C. | 149 | D. | 150 |
8.复数$\frac{-i}{3+i}$在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知$|{\overrightarrow a}$|=2,$|{\overrightarrow b}|$=$\sqrt{3}$,$\overrightarrow a$•$\overrightarrow b$=3,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
12.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
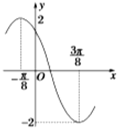 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,