题目内容
(1)化简:
(2)计算:tan70°cos10°(
tan20°-1).
sin(2π-α)cos(π+α)cos(
| ||||
cos(π-α)sin(3π-α)sin(-π-α)sin(
|
(2)计算:tan70°cos10°(
| 3 |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:(1)利用诱导公式化简,即可得出结论;
(2)切化弦,利用二倍角公式,化简可得结论.
(2)切化弦,利用二倍角公式,化简可得结论.
解答:
解:(1)
=
=tanα;
(2)tan70°cos10°(
tan20°-1)=tan70°cos10°•
=-
•cos10°•
=-1.
sin(2π-α)cos(π+α)cos(
| ||||
cos(π-α)sin(3π-α)sin(-π-α)sin(
|
| (-sinα)(-cosα)(-sinα)(-sinα) |
| (-cosα)sinαsinα(-cosα) |
(2)tan70°cos10°(
| 3 |
| sin60°sin20°-cos60°cos20° |
| cos60°cos20° |
=-
| cos20° |
| sin20° |
| cos80° | ||
|
点评:本题考查诱导公式,考查切化弦,二倍角公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
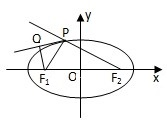 已知F1、F2是椭圆
已知F1、F2是椭圆