题目内容

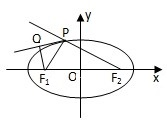已知F1、F2是椭圆
x2
172
+
y2
152
=1的左、右焦点，P是椭圆上任意一点，过F1引∠F1PF2的外角平分线的垂线，垂足为Q，则Q与短轴端点的最近距离为（　　）
A、4B、2C、8D、9
考点：椭圆的简单性质
专题：圆锥曲线中的最值与范围问题
分析：设F1Q的延长线交F2P的延长线于点M，由椭圆性质推导出|MF2|=34，由题意知OQ是△F1F2M的中位线，从而得到Q点的轨迹是以O为圆心，以17为半径的圆，由此能求出结果．
解答： 解：∵P是焦点为F1、F2的椭圆
x2
172
+
y2
152
=1上一点，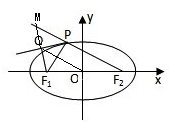
PQ为∠F1PF2的外角平分线，QF1⊥PQ，
设F1Q的延长线交F2P的延长线于点M，
∴|PM|=|PF1|，
∵|PF1|+|PF2|=2a=34，∴|MF2|=|PM|+|PF2|=2a=34，
由题意知OQ是△F1F2M的中位线，
∴|OQ|=a=17，
∴Q点的轨迹是以O为圆心，以17为半径的圆，
∴当点Q与y轴重合时，
Q与短轴端点取最近距离d=a-b=17-15=2．
故选：B．
点评：本题考查动点与椭圆短轴顶点的最小距离的求法，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
已知角a的终边经过点P（-4，m），且sina=-
3
5
，则m等于（　　）
A、-
11
3
B、
11
3
C、-3
D、3
设如果曲线C：
x=a+2cosθ
y=a+2sinθ
（θ为参数）上有且仅有两个点到原点的距离为2，则实数a的取值范围是（　　）
A、（-2
2
，0）
B、（0，2
2
）
C、（-2
2
，0）∪（0，2
2
）
D、（1，2
2
）
点（x，y）在直线 x+2y=3上移动，当2x+4y取最小值时，点（x，y）与原点的距离是（　　）
A、
3
5
4
B、
45
16
C、
3
2
4
D、
9
8
三位同学在研究函数f（x）=
x
1+|x|
（x∈R）时，分别给出下面三个结论：
①函数f（x）的值域为（-1，1）；②若x1≠x2，则一定有f（x1）≠f（x2）；③若规定f1（x）=f（x），fn+1（x）=f[fn（x）]，则fn（x）=
x
1+n|x|
对任意n∈N*恒成立．
你认为上述三个结论中正确的个数有（　　）
A、0个B、1个C、2个D、3个
曲线y=5sin(2x+
π
6
)与直线y=x的交点个数是（　　）
A、5B、6C、7D、8
已知
e1
，
e2
是平面内不共线的两个向量，
a
=2
e1
-3
e2
，
b
=λ
e1
+6
e2
．若
a
，
b
共线，则λ等于（　　）
A、-9B、-4C、4D、9
已知命题p：“x∈[-2，-
2
]时，x2-a≥0恒成立”；命题q：“方程x2+（a-3）x+a=0无实数根”．若“p∧q”是假命题，且“p∨q”是真命题，求实数a的取值范围．
（1）化简：
sin(2π-α)cos(π+α)cos(
π
2
+α)cos(
11π
2
-α)
cos(π-α)sin(3π-α)sin(-π-α)sin(
9π
2
+α)

（2）计算：tan70°cos10°(
3
tan20°-1)．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网