题目内容
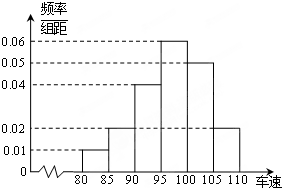 节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.(Ⅰ)请直接回答这种抽样方法是什么抽样方法?并估计出这40辆车速的中位数;
(Ⅱ)设车速在[80,85)的车辆为A1,A2,…,An(m为车速在[80,85)上的频数),车速在[85,90)的车辆为B1,B2,…,Bn(n为车速在[85,90)上的频数),从车速在[80,90)的车辆中任意抽取2辆共有几种情况?请列举出所有的情况,并求抽取的2辆车的车速都在[85,90)上的概率.
考点:古典概型及其概率计算公式,众数、中位数、平均数
专题:概率与统计
分析:(I)这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样;求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数;
(II)从图中可知,车速在[80,85)的车辆数和车速在[85,90)的车辆数.从车速在[80,90)的车辆中任抽取2辆,设车速在[80,85)的车辆设为a,b,车速在[85,90)的车辆设为c,d,e,f,列出各自的基本事件数,从而求出相应的概率即可.
(II)从图中可知,车速在[80,85)的车辆数和车速在[85,90)的车辆数.从车速在[80,90)的车辆中任抽取2辆,设车速在[80,85)的车辆设为a,b,车速在[85,90)的车辆设为c,d,e,f,列出各自的基本事件数,从而求出相应的概率即可.
解答:
解:(Ⅰ)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,
是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.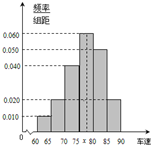
故调查公司在采样中,用到的是系统抽样,(2分)
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x-95)=0.5,
解得x=97.5,即中位数的估计值为97.5 (6分)
(Ⅱ)由(Ⅰ)得m1=0.01×5×40=2(辆),(7分)
m2=0.02×5×40=4(辆). …(8分)
∴所以车速在[80,90)的车辆中任意抽取2辆的所有情况是:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b,f),(c,d),
(c,e),(c,f),(d,e),(d,f),(e,f),共有15种情况. …(10分)
车速都在[85,90)上的2辆车的情况有6种.
所以车速都在[85,90)上的2辆车的概率是
=
. …(12分)
是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.

故调查公司在采样中,用到的是系统抽样,(2分)
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x-95)=0.5,
解得x=97.5,即中位数的估计值为97.5 (6分)
(Ⅱ)由(Ⅰ)得m1=0.01×5×40=2(辆),(7分)
m2=0.02×5×40=4(辆). …(8分)
∴所以车速在[80,90)的车辆中任意抽取2辆的所有情况是:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b,f),(c,d),
(c,e),(c,f),(d,e),(d,f),(e,f),共有15种情况. …(10分)
车速都在[85,90)上的2辆车的情况有6种.
所以车速都在[85,90)上的2辆车的概率是
| 6 |
| 15 |
| 2 |
| 5 |
点评:解决频率分布直方图的有关特征数问题,利用众数是最高矩形的底边中点;中位数是左右两边的矩形的面积相等的底边的值;平均数等于各个小矩形的面积乘以对应的矩形的底边中点的和.此题把统计和概率结合在一起,比较新颖,也是高考的方向,应引起重视.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆