题目内容
如图，在平面直角坐标系xOy中，椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
（1）求椭圆的方程；
（2）求AB+CD的取值范围．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由题意知，e=
=
，CD=7-2a，再由点(c，
)在椭圆上，能求出椭圆的方程．
（2）当两条弦中一条斜率为0时，另一条弦的斜率不存在时，AB+CD=7；当两弦斜率均存在且不为0时，设A（x1，y1），B（x2，y2），设直线AB的方程为y=k（x-1），直线CD的方程为y=-
(x-1)．由此能求出AB+CD=
+
=
，从而能求出AB+CD的取值范围．
| c |
| a |
| 1 |
| 2 |
| 7-4c |
| 2 |
（2）当两条弦中一条斜率为0时，另一条弦的斜率不存在时，AB+CD=7；当两弦斜率均存在且不为0时，设A（x1，y1），B（x2，y2），设直线AB的方程为y=k（x-1），直线CD的方程为y=-
| 1 |
| k |
| 12(k2+1) |
| 3+4k2 |
| 12(k2+1) |
| 3k2+4 |
| 84(k2+1)2 |
| (3+4k2)(3k2+4) |
解答：
解：（1）由题意知，e=
=
，CD=7-2a，
所以a2=4c2，b2=3c2，…2分
因为点(c，
)在椭圆上，
即
+
=1，
解得c=1．
所以椭圆的方程为
+
=1．…6分
（2）①当两条弦中一条斜率为0时，另一条弦的斜率不存在，
由题意知AB+CD=7；…7分
②当两弦斜率均存在且不为0时，设A（x1，y1），B（x2，y2），
且设直线AB的方程为y=k（x-1），
则直线CD的方程为y=-
(x-1)．
将直线AB的方程代入椭圆方程中，
并整理得（3+4k2）x2-8k2x+4k2-12=0，
所以x1=
，x2=
，
所以AB=
|x1-x2|=
．…10分
同理，CD=
=
．
所以AB+CD=
+
=
，…12分
令t=k2+1，则t＞1，3+4k2=4t-1，3k2+4=3t+1，
设f(t)=
=-
+
+12=-(
-
)2+
，
因为t＞1，所以
∈(0，1)，
所以f(t)∈(12，
]，
所以AB+CD=
∈[
，7)．
综合①与②可知，AB+CD的取值范围是[
，7]． …16分．
| c |
| a |
| 1 |
| 2 |
所以a2=4c2，b2=3c2，…2分
因为点(c，
| 7-4c |
| 2 |
即
| c2 |
| 4c2 |
(
| ||
| 3c2 |
解得c=1．
所以椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）①当两条弦中一条斜率为0时，另一条弦的斜率不存在，
由题意知AB+CD=7；…7分
②当两弦斜率均存在且不为0时，设A（x1，y1），B（x2，y2），
且设直线AB的方程为y=k（x-1），
则直线CD的方程为y=-
| 1 |
| k |
将直线AB的方程代入椭圆方程中，
并整理得（3+4k2）x2-8k2x+4k2-12=0，
所以x1=
4k2-6
| ||
| 3+4k2 |
4k2+6
| ||
| 3+4k2 |
所以AB=
| k2+1 |
| 12(k2+1) |
| 3+4k2 |
同理，CD=
12(
| ||
3+
|
| 12(k2+1) |
| 3k2+4 |
所以AB+CD=
| 12(k2+1) |
| 3+4k2 |
| 12(k2+1) |
| 3k2+4 |
| 84(k2+1)2 |
| (3+4k2)(3k2+4) |
令t=k2+1，则t＞1，3+4k2=4t-1，3k2+4=3t+1，
设f(t)=
| (4t-1)(3t+1) |
| t2 |
| 1 |
| t2 |
| 1 |
| t |
| 1 |
| t |
| 1 |
| 2 |
| 49 |
| 4 |
因为t＞1，所以
| 1 |
| t |
所以f(t)∈(12，
| 49 |
| 4 |
所以AB+CD=
| 84 |
| f(t) |
| 48 |
| 7 |
综合①与②可知，AB+CD的取值范围是[
| 48 |
| 7 |
点评：本题考查椭圆的方程的求法，考查两条线段和的取值范围的求法，解题时要认真审题，注意分类讨论思想的合理运用．
练习册系列答案
相关题目
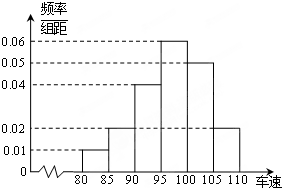节日期间，高速公路车辆较多，某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序，随机抽取第一辆汽车后，每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．
已知函数f（x）=Asin（wx+φ）+b，（w＞0），|φ|＜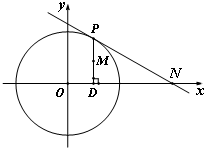
如图，在圆O：x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．设M为线段PD的中点．