题目内容
已知函数f（x）cosx（cosx-
sinx）（x∈R）
（Ⅰ）写出f（x）的单调减区间；
（Ⅱ）在△ABC中，A、B、C所对的边分别是a、b、c，若f（A）=0，A∈（0，
），且（1+
）c=2b．求角C．
| 3 |
（Ⅰ）写出f（x）的单调减区间；
（Ⅱ）在△ABC中，A、B、C所对的边分别是a、b、c，若f（A）=0，A∈（0，
| π |
| 2 |
| 3 |
考点：三角函数中的恒等变换应用,余弦定理
专题：三角函数的图像与性质,解三角形
分析：（Ⅰ）通过二倍角公式和两角和公式对函数解析式进行化简，然后利用余弦定理的图象和性质求得其单调减区间．
（Ⅱ）利用f（A）=0求得cos（2A+
）的值，进而求得A，然后通过正弦定理把（1+
）c=2b转化成角的正弦的关系式，化简整理求得tanC的值，进而求得C．
（Ⅱ）利用f（A）=0求得cos（2A+
| π |
| 3 |
| 3 |
解答：
解：（Ⅰ）f（x）=cosx（cosx-
sinx）=cos2x-
sinxcosx=
cos2x+
-
sin2x=cos（2x+
）+
∴当2kπ≤2x+
≤2kπ+π，k∈Z时，即kπ-
x≤kπ+
时，函数单调减，
∴函数f（x）的单调递减区间为：[kπ-
，kπ+
]（k∈Z）．
（Ⅱ）由（Ⅰ）知，f（x）=cos（2x+
）+
∴f（A）=cos（2A+
）+
=0
∴cos（2A+
）=-
，
∵A∈（0，
），
∴
＜2A+
＜
，
∴2A+
=
，
∴A=
．
∵（1+
）c=2b．
∴（1+
）sinC=2sinB，
∴（1+
）sinC=2sin（π-
-C）=2sin（
-C）=2（sin
cosC-cos
sinC）=cosC+
sinC，
∴cosC=sinC，即tanC=1，
∴C=
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 2 |
∴当2kπ≤2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
∴函数f（x）的单调递减区间为：[kπ-
| π |
| 6 |
| π |
| 3 |
（Ⅱ）由（Ⅰ）知，f（x）=cos（2x+
| π |
| 3 |
| 1 |
| 2 |
∴f（A）=cos（2A+
| π |
| 3 |
| 1 |
| 2 |
∴cos（2A+
| π |
| 3 |
| 1 |
| 2 |
∵A∈（0，
| π |
| 2 |
∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴2A+
| π |
| 3 |
| 2π |
| 3 |
∴A=
| π |
| 6 |
∵（1+
| 3 |
∴（1+
| 3 |
∴（1+
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 3 |
∴cosC=sinC，即tanC=1，
∴C=
| π |
| 4 |
点评：本题主要考查三角函数恒等变换的应用，正弦定理的应用．注重对基础知识和数学运算能力的考查．
练习册系列答案
相关题目
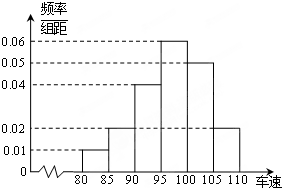节日期间，高速公路车辆较多，某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序，随机抽取第一辆汽车后，每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．