题目内容
已知函数f(x)=alnx-x2,函数f(x)在x=1处取得极值.
(1)求实数a的值;
(2)函数g(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,又g′(x)是函数g(x)的导函数,证明:g′(
)<0.
(1)求实数a的值;
(2)函数g(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,又g′(x)是函数g(x)的导函数,证明:g′(
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)根据f(x)在x=1处取得极值知f′(1)=a-2=0,解方程即可求实数a的值;
(2)由题意可得,f(x)-mx=0有两个实根x1,x2,化简可得x1+x2+m=
,从而不等式g′(
)<0,可化为
>ln
,令
=t,则0<t<1,令h(t)=2-
-lnt,利用导数推出在(0,1)上,h′(t)<0,h(t)单调递减,h(t)>h(1)=0,从而不等式可证.
(2)由题意可得,f(x)-mx=0有两个实根x1,x2,化简可得x1+x2+m=
2ln
| ||
| x1-x2 |
| x1+x2 |
| 2 |
| 2(x1-x2) |
| x1+x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| 4 |
| t+1 |
解答:
(1)解:∵f(x)=alnx-x2,
∴f′(x)=
-2x,
∵函数f(x)在x=1处取得极值,
∴f′(1)=a-2=0,
∴a=2;
(2)证明:g(x)=f(x)-mx=2lnx-x2-mx,
∴g′(x)=
-2x-m,
∵函数g(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),
∴2lnx1-x12-mx1=0,2lnx2-x22-mx2=0,
两式相减可得2ln
-(x1+x2)(x1-x2)-m(x1-x2)=0
∴x1+x2+m=
,
g′(
)=
-(x1+x2+m)=
-
,
要证g′(
)<0,
即证
-
<0,
即证
>ln
,
即证
-ln
=2-
-ln
>0…①,
令
=t,则0<t<1,
令h(t)=2-
-lnt,
则h′(t)=
-
,
由h′(t)=0得,t=1,
∴当0<t<1时h′(t)<0,h(t)单调递减,
∴h(t)>h(1)=0,
∴①式得证.
∴f′(x)=
| a |
| x |
∵函数f(x)在x=1处取得极值,
∴f′(1)=a-2=0,
∴a=2;
(2)证明:g(x)=f(x)-mx=2lnx-x2-mx,
∴g′(x)=
| 2 |
| x |
∵函数g(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),
∴2lnx1-x12-mx1=0,2lnx2-x22-mx2=0,
两式相减可得2ln
| x1 |
| x2 |
∴x1+x2+m=
2ln
| ||
| x1-x2 |
g′(
| x1+x2 |
| 2 |
| 4 |
| x1+x2 |
| 4 |
| x1+x2 |
2ln
| ||
| x1-x2 |
要证g′(
| x1+x2 |
| 2 |
即证
| 4 |
| x1+x2 |
2ln
| ||
| x1-x2 |
即证
| 2(x1-x2) |
| x1+x2 |
| x1 |
| x2 |
即证
2(
| ||
|
| x1 |
| x2 |
| 4 | ||
|
| x1 |
| x2 |
令
| x1 |
| x2 |
令h(t)=2-
| 4 |
| t+1 |
则h′(t)=
| 4 |
| (t+1)2 |
| 1 |
| t |
由h′(t)=0得,t=1,
∴当0<t<1时h′(t)<0,h(t)单调递减,
∴h(t)>h(1)=0,
∴①式得证.
点评:本题主要考查利用导数研究函数的单调性,利用函数的单调性求函数在闭区间上的最值,用分析法证明不等式,体现了转化的数学思想,属于难题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
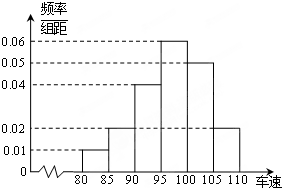 节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.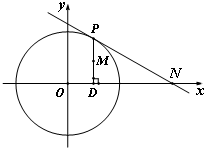 如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.
如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.