题目内容
投掷质地均匀的红、蓝两颗骰子,观察出现的点数,并记红色骰子出现的点数为m,蓝色骰子出现的点数为n.试就方程组
解答下列问题.
(Ⅰ)求方程组只有一个解的概率;
(Ⅱ)求方程组只有正数解的概率.
|
(Ⅰ)求方程组只有一个解的概率;
(Ⅱ)求方程组只有正数解的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由题意知本题是一个古典概型,事件(m,n)的基本事件有36个,方程组只有一个解,需满足2m-n≠0,即n≠2m,而n=2m的事件有(1,2),(2,4),(3,6)共3个,根据古典概型概率公式得到结果.
(2)由题意知本题是一个古典概型,事件(m,n)的基本事件有36个,方程组只有正数解整理出结果,列举出所有满足条件的事件,根据概率公式得到结果.
(2)由题意知本题是一个古典概型,事件(m,n)的基本事件有36个,方程组只有正数解整理出结果,列举出所有满足条件的事件,根据概率公式得到结果.
解答:
解:(1)由题意知本题是一个古典概型,事件(m,n)的基本事件有36个,
由方程组
可得
方程组只有一个解,需满足2m-n≠0,
即n≠2m,而n=2m的事件有(1,2),(2,4),(3,6)共3个,
所以方程组只有一个解的概率为P1=1-
=
.
(2)方程组只有正数解,需2m-n≠0且
.
即
或
其包含的事件有13个:(2,1),(3,1),(4,1),(5,1),(6,1),
(2,2),(3,2),(4,2),(5,2),(6,2),(1,4),(1,5),(1,6).
∴所求的概率为
.
由方程组
|
可得
|
方程组只有一个解,需满足2m-n≠0,
即n≠2m,而n=2m的事件有(1,2),(2,4),(3,6)共3个,
所以方程组只有一个解的概率为P1=1-
| 3 |
| 36 |
| 11 |
| 12 |
(2)方程组只有正数解,需2m-n≠0且
|
即
|
|
其包含的事件有13个:(2,1),(3,1),(4,1),(5,1),(6,1),
(2,2),(3,2),(4,2),(5,2),(6,2),(1,4),(1,5),(1,6).
∴所求的概率为
| 13 |
| 36 |
点评:本题考查古典概型,考查解方程组,是一个综合题,概率问题往往同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点.

练习册系列答案
相关题目
执行如图所示的程序框图.若输入a=3,则输出i的值是( )


| A、2 | B、3 | C、4 | D、5 |
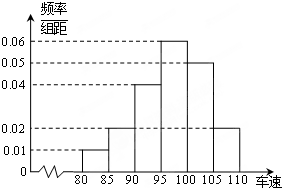 节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.