题目内容
从6名短跑运动员中选出4人参加4×100m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒.
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒.
考点:计数原理的应用
专题:排列组合
分析:(1)利用分类计数原理,分甲不参赛和参赛两类,在根据特出元素特殊处理原则,问题得以解决.
(2)甲不能跑第一棒,乙不能跑第四棒,以乙跑不跑第一棒分两类.
(2)甲不能跑第一棒,乙不能跑第四棒,以乙跑不跑第一棒分两类.
解答:
解 (1),甲不一定被选中,因此需分两类:
第1类,甲不参赛有A种排法
;
第2类,甲参赛,因只有两个位置可供选择,故有A
种排法;其余5人占3个位置有A
种排法,故有A
A
种方案.
所以有A
+A
A
=240种参赛方案.
(2)从6名短跑运动员中选出4人,甲不能跑第一棒,乙不能跑第四棒,以乙跑不跑第一棒分两类.
第1类,乙跑第一棒有A
A
=60种排法;
第2类,乙不跑第一棒有A
A
A
=192种排法.
故共有60+192=252种参赛方案.
第1类,甲不参赛有A种排法
| A | 4 5 |
第2类,甲参赛,因只有两个位置可供选择,故有A
1 2 |
3 5 |
1 2 |
3 5 |
所以有A
4 5 |
1 2 |
3 5 |
(2)从6名短跑运动员中选出4人,甲不能跑第一棒,乙不能跑第四棒,以乙跑不跑第一棒分两类.
第1类,乙跑第一棒有A
1 1 |
3 5 |
第2类,乙不跑第一棒有A
1 4 |
1 4 |
2 4 |
故共有60+192=252种参赛方案.
点评:本题主要考查了分类计数原理,关键是如何分类,以哪个特殊元素进行分类,分类是要不重不漏.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
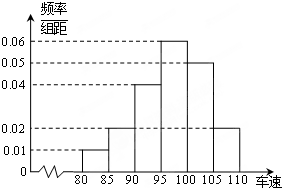 节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.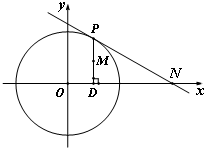 如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.
如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.