题目内容
已知点P(1,m)在抛物线C:y2=2Px(P>0)上,F为焦点,且|PF|=3.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点T(4,0)的直线l交抛物线C于A,B两点,O为坐标原点.
(ⅰ)求
•
的值;
(ⅱ)若以A为圆心,|AT|为半径的圆与y轴交于M,N两点,求△MNF的面积.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点T(4,0)的直线l交抛物线C于A,B两点,O为坐标原点.
(ⅰ)求
| OA |
| OB |
(ⅱ)若以A为圆心,|AT|为半径的圆与y轴交于M,N两点,求△MNF的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由抛物线定义得:|PF|=1+
=3,由此能求出抛物线C的方程.
(II)(i)依题意设过点T(4,0)的直线l的方程为x=ty+4,由
,得y2-8ty-32=0,由此利用韦达定理能求出
•
=-16.
(ii)设A(x1,y1),M(0,yM),N(0,yN),则y12=8x1,以A为圆心,|AT|为半径的圆的方程为(x-x1)2+(y-y1)2=(4-x1)2+y12,由此能求出△MNF的面积.
| p |
| 2 |
(II)(i)依题意设过点T(4,0)的直线l的方程为x=ty+4,由
|
| OA |
| OB |
(ii)设A(x1,y1),M(0,yM),N(0,yN),则y12=8x1,以A为圆心,|AT|为半径的圆的方程为(x-x1)2+(y-y1)2=(4-x1)2+y12,由此能求出△MNF的面积.
解答:
满分(12分).
解:(I)抛物线C:y2=2px(p>0),
∴焦点F(
,0).…(1分)
由抛物线定义得:|PF|=1+
=3,
解得p=4,
∴抛物线C的方程为y2=8x.…(3分)
(II)(i)依题意可设过点T(4,0)的直线l的方程为x=ty+4,…(4分)
由
,得y2-8ty-32=0,…(5分)
设A(x1,y1),B(x2,y2),
则y1+y2=8t,y1y2=-32,…(6分)
∴x1•x2=
y12•
y22=16,…(7分)
∴
•
=x1 x2+y1 y2=16-32=-16.…(8分)
(ii)设A(x1,y1),M(0,yM),N(0,yN),则y12=8x1,①
以A为圆心,|AT|为半径的圆的方程为(x-x1)2+(y-y1)2=(4-x1)2+y12,…(9分)
令x=0,则x1 2+(y-y1)2=(4-x1)2+y12,②
把①代入②得(y-y1)2=16,
∴y=y1+4或y=y1-4,
∴|MN|=|yM-yN|=8,…(11分)
∴S△MNF=
•|MN|•|OF|=
•8•2=8.…(12分)
解:(I)抛物线C:y2=2px(p>0),
∴焦点F(
| p |
| 2 |
由抛物线定义得:|PF|=1+
| p |
| 2 |
解得p=4,
∴抛物线C的方程为y2=8x.…(3分)
(II)(i)依题意可设过点T(4,0)的直线l的方程为x=ty+4,…(4分)
由
|
设A(x1,y1),B(x2,y2),
则y1+y2=8t,y1y2=-32,…(6分)
∴x1•x2=
| 1 |
| 8 |
| 1 |
| 8 |
∴
| OA |
| OB |
(ii)设A(x1,y1),M(0,yM),N(0,yN),则y12=8x1,①
以A为圆心,|AT|为半径的圆的方程为(x-x1)2+(y-y1)2=(4-x1)2+y12,…(9分)
令x=0,则x1 2+(y-y1)2=(4-x1)2+y12,②
把①代入②得(y-y1)2=16,
∴y=y1+4或y=y1-4,
∴|MN|=|yM-yN|=8,…(11分)
∴S△MNF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查直线、圆、抛物线等基础知识及直线与圆锥曲线的位置关系;考查运算求解能力、推理论证能力;考查特殊与一般的思想、化归与转化思想.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
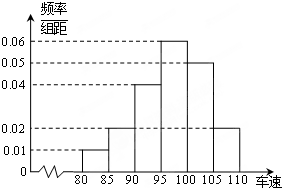 节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图. 已知函数f(x)=Asin(wx+φ)+b,(w>0),|φ|<
已知函数f(x)=Asin(wx+φ)+b,(w>0),|φ|<