题目内容
在△ABC中，A、B、C的对边分别是a，b，c，且bcosB是acosC，ccosA的等差中项，则角B= ．
考点：等差数列的性质
专题：等差数列与等比数列,解三角形
分析：由题意可得2bcosB=acosC+ccosA，结合正弦定理和三角函数公式可得cosB=
，由三角形内角的范围可得B值．
| 1 |
| 2 |
解答：
解：∵bcosB是acosC，ccosA的等差中项，
∴2bcosB=acosC+ccosA，
由正弦定理可得2sinBcosB=sinAcosC+sinCcosA，
即2sinBcosB=sin（A+C）=sinB，
又∵sinB＞0，上式两边同除以sinB可得cosB=
，
∵0＜B＜π，∴B=
故答案为：
．
∴2bcosB=acosC+ccosA，
由正弦定理可得2sinBcosB=sinAcosC+sinCcosA，
即2sinBcosB=sin（A+C）=sinB，
又∵sinB＞0，上式两边同除以sinB可得cosB=
| 1 |
| 2 |
∵0＜B＜π，∴B=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查等差数列的性质和解三角形，属中档题．
练习册系列答案
相关题目
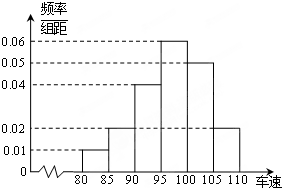节日期间，高速公路车辆较多，某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序，随机抽取第一辆汽车后，每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．
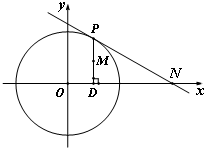如图，在圆O：x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．设M为线段PD的中点．