题目内容
设全集U=R,集合A={x|
≥0},B={x|0<x+1<4},则A∩B等于( )
| x+1 |
| x-2 |
| A、[-1,3) |
| B、(0,2] |
| C、(1,2] |
| D、(2,3) |
考点:交集及其运算
专题:集合
分析:求出A与B中不等式的解集确定出A与B,找出A与B的交集即可.
解答:
解:由A中的不等式变形得:(x+1)(x-2)≥0,且x-2≠0,
解得:x≤-1或x>2,即A=(-∞,-1]∪(2,+∞),
由B中的不等式解得:-1<x<3,即B=(-1,3),
则A∩B=(2,3).
故选:D.
解得:x≤-1或x>2,即A=(-∞,-1]∪(2,+∞),
由B中的不等式解得:-1<x<3,即B=(-1,3),
则A∩B=(2,3).
故选:D.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p:a,b为异面直线,命题q:直线a,b不相交,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
 给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )
给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )| A、i≤10?,p=p+i-1 |
| B、i≤9?,p=p+i |
| C、i≤10?,p=p+i |
| D、i≤11?,p=p+i |
设a=40.6,b=0.63,c=log0.63,则a、b、c的大小关系是( )
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
有4个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在复平面内,满足条件z•(1+i)=2的复数z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

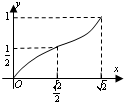
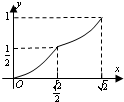
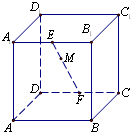 如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )
如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )