题目内容
已知命题p：a，b为异面直线，命题q：直线a，b不相交，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据直线的位置关系，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若a，b为异面直线，则直线a，b不相交，充分性成立，
若a，b为异面直线，则直线a，b不相交或者平行，必要性不成立．
故p是q的充分不必要条件，
故选：A
若a，b为异面直线，则直线a，b不相交或者平行，必要性不成立．
故p是q的充分不必要条件，
故选：A
点评：本题主要考查充分条件和必要条件的判断，利用空集直线的位置关系是解决本题的关键．
练习册系列答案
相关题目
设变量x、y满足约束条件：
，则目标函数z=5x+3y的最大值为（ ）
|
| A、18 | ||
| B、17 | ||
| C、27 | ||
D、
|
设x、y满足约束条件
，若目标函数z=x+y的最大值为m，则y=sin（mx+
）的图象向右平移
后的表达式为（ ）
|
| π |
| 3 |
| π |
| 6 |
| A、y=sinx | ||
| B、y=sin2x | ||
C、y=sin（x+
| ||
D、y=sin（2x+
|
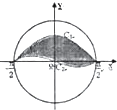如图，在一圆形水域内有一片“枯叶”，它的边界由曲线C1：f（x）=cosx与曲线C2：g（x）=| 2 |
| π |
| π2 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，边a，b，c所对的角分别为A，B，C，若a=1，A=30°，B=60°，则b=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知变量x，y满足约束条件
，则目标函数z=2x+y的最大值是（ ）
|
| A、-4 | B、0 | C、2 | D、4 |
设全集U=R，集合A={x|
≥0}，B={x|0＜x+1＜4}，则A∩B等于（ ）
| x+1 |
| x-2 |
| A、[-1，3） |
| B、（0，2] |
| C、（1，2] |
| D、（2，3） |