题目内容
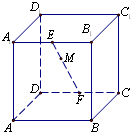如图：正方体ABCD-A1B1C1D1的棱长为1，E，F分别是棱A1B1，CD的中点，点M是EF的动点，FM=x，过点M、直线AB的平面将正方体分成上下两部分，记下面那部分的体积为V（x），则函数V（x）的大致图象是（ ）A、 |
B、 |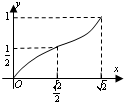
C、 |
D、 |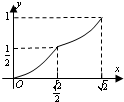
考点：函数的图象
专题：函数思想
分析：本题关键是理解，体积V（x）的变化是随变x的变化而怎样变化的，可以找列出V关于x的关系式，利用相似比就可以找到它们的关系，从而得到答案，当然此题也可以从体积的变化快慢来理解得到答案．
解答：
解：如图：（1）当0＜x＜
时，过点M、直线AB作平面交CC1，DD1于点P、Q，则四边形ABPQ为矩形，
此时，截面下面那部分是三棱矩ADQ-BCP，
∵FM=CM1=x，如图：B1C=
，△BB1M1∽△PM1C，由相似比得，
=
，
=
，∴CP=
，
∴三棱矩ADQ-BCP的体积V（x）=S△BCP•AB=
×
×1×1=
；
（2）当
＜x＜
时，过点M、直线AB作平面交B1C1，A1D1于点P、Q，则四边形ABPQ为矩形，
此时，截面下面那部分是四棱矩ADQA1-BCPB1，
∵FM=x，由相似比知C1P=
，
∴四棱矩ADQA1-BCPB1的体积V（x）=
(
+1)×1×1=
．
∴V（X）=
．
由解析式，知V（x）的图象为C．
故选：C．
| ||
| 2 |
此时，截面下面那部分是三棱矩ADQ-BCP，
∵FM=CM1=x，如图：B1C=
| 2 |
| CP |
| BB1 |
| MC |
| B1M |
| CP |
| 1 |
| x | ||
|
| x | ||
|
∴三棱矩ADQ-BCP的体积V（x）=S△BCP•AB=
| 1 |
| 2 |
| x | ||
|
| x | ||
2(
|
（2）当
| ||
| 2 |
| 2 |
此时，截面下面那部分是四棱矩ADQA1-BCPB1，
∵FM=x，由相似比知C1P=
2x-
| ||
| x |
∴四棱矩ADQA1-BCPB1的体积V（x）=
| 1 |
| 2 |
2x-
| ||
| x |
3x-
| ||
| 2x |
∴V（X）=
|
由解析式，知V（x）的图象为C．
故选：C．
点评：本题考查空间相象能力，函数思想，关键是要求理解变量与变量之间的关系．属于较难题．
练习册系列答案
相关题目
在△ABC中，边a，b，c所对的角分别为A，B，C，若a=1，A=30°，B=60°，则b=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
给定区域D：
，令点集M={（x0，y0）∈D|x0，y0∈Z}，且点（x0，y0）是目标函数z=x+y在区域D上取最值的最优解}，则集合M中的点最多可确定直线的条数是（ ）
|
| A、4条 | B、5条 | C、6条 | D、10条 |
设全集U=R，集合A={x|
≥0}，B={x|0＜x+1＜4}，则A∩B等于（ ）
| x+1 |
| x-2 |
| A、[-1，3） |
| B、（0，2] |
| C、（1，2] |
| D、（2，3） |
若点P在曲线y=-x2+x+2上移动，且P点横坐标取值范围是[0，
]，经过点P的切线的倾斜角为α，则α的取值范围是（ ）
| 1 |
| 2 |
A、[0，
| ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
设变量x，y满足约束条件
，则目标函数z=x-2y的最大值为（ ）
|
A、
| ||
| B、1 | ||
C、-
| ||
| D、-2 |