题目内容

设a=40.6，b=0.63，c=log0.63，则a、b、c的大小关系是（　　）
A、a＜b＜c
B、b＜a＜c
C、b＜c＜a
D、c＜b＜a
考点：不等关系与不等式,对数的运算性质
专题：函数的性质及应用
分析：依据对数的性质，指数的性质，分别确定a、b、c数值的大小，然后判定结果即可．
解答： 解：由于a=40.6＞40=1，
0＜b=0.63＜0.60=1，
c=log0.63＜log0.61=0，
∴40.3＞0.63＞log0.63，
∴c＜b＜a
故选：D．
点评：本题主要考查对数函数、指数函数的单调性，属于基础题，常规题．
练习册系列答案
相关题目
函数y=2x的反函数为g（x），则g（2）=
 
．
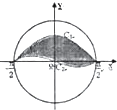如图，在一圆形水域内有一片“枯叶”，它的边界由曲线C1：f（x）=cosx与曲线C2：g（x）=
2
π
x-sinx围成，圆的方程为：x2+y2=
π2
4
，假设“枯叶”在水中保持静止，现有一小孩向水中投掷一颗沙粒，则此沙粒恰好砸中“枯叶”的概率为（　　）
A、
2
π2
B、
8
π3
C、
8
π2
D、
4
π3
已知变量x，y满足约束条件
x+y≤1
x+1≥0
x-y≤1
，则目标函数z=2x+y的最大值是（　　）
A、-4B、0C、2D、4
已知集合A={x|0＜x＜2}，B={x|y=
1-x2
}，则A∪∁RB=（　　）
A、（0，1）
B、（1，2）
C、（-∞，-1）∪（0，+∞）
D、（-∞，-1）∪（1，+∞）
设全集U=R，集合A={x|
x+1
x-2
≥0}，B={x|0＜x+1＜4}，则A∩B等于（　　）
A、[-1，3）
B、（0，2]
C、（1，2]
D、（2，3）
若i（i是虚数单位）是关于x的方程x2+px+q=0（p，q∈R）的一个根，则p-q=（　　）
A、-1B、0C、-2D、1
在曲线y=x2的切线的倾斜角为
3π
4
的点为（　　）
A、（0，0）
B、（
1
2
，
1
4
）
C、（-
1
2
，
1
4
）
D、（
1
2
，
1
4
）或（-
1
2
，
1
4
）
已知函数f（x）=（a+1）lnx+ax2+1，且a≤-2．
证明：对任意的x1，x2∈（0，+∞），|f（x1）-f（x2）|≥4|x1-x2|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网