题目内容
已知函数f（x）=
sin（2x+
），
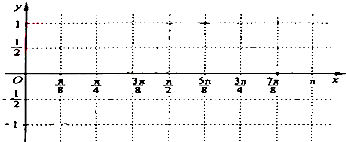
（1）借助”五点作图法”画出函数f（x）在[0，
]上的简图，
（2）依图写出函数f（x）在[0，
]上的递增区间．
| 2 |
| π |
| 4 |
（1）借助”五点作图法”画出函数f（x）在[0，
| 7π |
| 8 |
（2）依图写出函数f（x）在[0，
| 7π |
| 8 |
考点：五点法作函数y=Asin（ωx+φ）的图象,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）分别令2x+
=0，
，π，
，2π，得到相应的x的值及y的值，再描点即可；
（2）由图可得该函数的增区间．
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
（2）由图可得该函数的增区间．
解答：
解：可先画出区间[-
，
]的图象，再截取所需．
列表
图象如图，
注意f（0）=1，由图象可知函数在区间[0，
]上的单调递增区间是[0，
]，[
，
]．
| π |
| 8 |
| 7π |
| 8 |
列表
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 |
|
0 | -
|
0 |
注意f（0）=1，由图象可知函数在区间[0，
| 7π |
| 8 |
| π |
| 8 |
| 5π |
| 8 |
| 7π |
| 8 |
点评：本题考查五点法作函数y=Asin（ωx+φ）的图象，属于中档题．
练习册系列答案
相关题目
设全集U=R，集合A={x|
≥0}，B={x|0＜x+1＜4}，则A∩B等于（ ）
| x+1 |
| x-2 |
| A、[-1，3） |
| B、（0，2] |
| C、（1，2] |
| D、（2，3） |
如图1，在边长为3的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A-BCF，其中BC=