Question

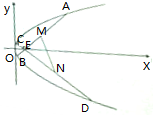已知点E（m，0）为抛物线y²=4x内的一个定点，过E作斜率分别为k₁、k₂的两条直线交抛物线于点A、B、C、D，且M、N分别是AB、CD的中点．
（1）若m=1，k₁k₂=-1，求△EMN面积的最小值；
（2）若k₁+k₂=1，求证：直线MN过定点．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线中的最值与范围问题

分析：（1）不妨设AB的斜率k₁=k＞0，求出CD的斜率k₂=-

1

k

＜0，利用点斜式方程求出直线AB、CD的方程，与抛物线方程联立消x得关于y的一元二次方程，根据韦达定理即可求得中点M、N的坐标，利用点斜式方程求出直线MN的方程，再求出直线MN与x轴的交点坐标，可得△EMN的面积，利用基本不等式求△MCD面积的最小值；
（2）不妨设AB的斜率k₁=k，求出CD的斜率k₂=1-m，利用点斜式方程求出直线AB、CD的方程，与抛物线方程联立消x得关于y的一元二次方程，根据韦达定理即可求得中点M、N的坐标，利用点斜式方程求出直线MN的方程，化简后求出直线过的定点坐标．

解答： （1）解：由题意不妨设AB的斜率k₁=k＞0，则CD的斜率k₂=-

1

k

＜0，
又m=1，则点E（1，0），
所以AB的直线方程是：y=k（x-1），CD的直线方程是y=-

1

k

（x-1），
设A（x₁，y₁），B（x₂，y₂），
由

y=k(x-1) y2=4x

得，k²x²-（2k²+4）x+k²=0，
则x1+x2=

2k2+4

k2

=2+

4

k2

，x₁x₂=1，
所以y₁+y₂=k（x₁-1）+k（x₂-1）=k（2+

4

k2

）-2k=

4

k

，
因为M是AB的中点，所以点M（1+

2

k2

，

2

k

），
同理可得，点N（1+2k²，-2k），
所以直线MN的方程是：y+2k=

2 k +2k

1+ 2 k2 -1-2k2

（x-1-2k²），
即y+2k=

1 k +k

1 k2 -k2

（x-1-2k²），令y=0，得x=3，
则直线MN与x轴的交点是（3，0），
所以△EMN面积S=

1

2

（3-1）（

2

k

+2k）=

2

k

+2k≥2

2 k ×2k

=4，
当且仅当

2

k

=2k时取等号，此时k=1，
所以△EMN面积的最小值是4；
（2）证明：由题意知，k₁+k₂=1，
不妨设AB的斜率k₁=k，则CD的斜率k₂=1-k，
所以AB的直线方程是：y=k（x-m），CD的直线方程是y=（1-k）（x-m），
设A（x₁′，y₁′），B（x₂′，y₂′），
由

y=k(x-m) y2=4x

得，k²x²-（2k²m+4）x+k²m²=0，
则x1′+x2′=

2k2m+4

k2

=2m+

4

k2

，x₁′x₂′=m²，
所以y₁′+y_2′=k（x₁′-m）+k（x₂′-m）=k（2m+

4

k2

）-2km=

4

k

，
因为M是AB的中点，所以点M（m+

2

k2

，

2

k

），
同理可得，点N（m+

2

(1-k)2

，

2

1-k

），
所以直线MN的方程是：y-

2

k

=

2 k - 2 1-k

2 k2 - 2 (1-k)2

（x-m-

2

k2

），
化简得，y=（k-k²）（x-m）+2，令x=m，得y=2，
所以直线MN过定点（m，2）．

点评：本题主要考查抛物线的几何性质，直线方程的求解，以及直线与抛物线的位置关系等基础知识，同时考查解析几何的基本思想方法和运算求解能力．