题目内容
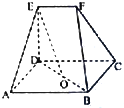 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=| 1 |
| 2 |
(Ⅰ)求证:EO∥平面BCF;
(Ⅱ)求几何体ABCDEF的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)取BC的中点G,连接OG,FG,可证得:EOGF为平行四边形,即EO∥FG,进而运用线面平行的判定定理,即可得证;
(Ⅱ)将多面体分割成棱锥F-ABCD和F-ADE,进而运用三棱锥的体积公式即可得到体积.
(Ⅱ)将多面体分割成棱锥F-ABCD和F-ADE,进而运用三棱锥的体积公式即可得到体积.
解答:
证明:(Ⅰ)取BC的中点G,连接OG,FG,
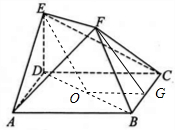
∵O为为BD中点,
∴OG∥CD,且OG=
CD,
又∵EF∥DC,EF=
AB=
CD,
∴EF∥OG,且EF=OG,
∴四边形EOGF为平行四边形,即EO∥FG,
又∵EO?平面BCF,FG?平面BCF,
∴EO∥平面BCF;
(Ⅱ)∵ED⊥平面ABCD,EF∥DC,
故F点到底面ABCD的距离等于ED=2,
故棱锥F-ABCD的体积为:
×2×4×2=
,
又∵ED⊥平面ABCD,平面ABCD为矩形,
故CD⊥平面ADE,
又由EF∥DC,
∴EF⊥平面ADE,
∴棱锥F-ADE的体积为:
×
×2×2×2=
,
又∵几何体ABCDEF可分割成棱锥F-ABCD和F-ADE,
故几何体ABCDEF的体积V=
+
=
.

∵O为为BD中点,
∴OG∥CD,且OG=
| 1 |
| 2 |
又∵EF∥DC,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥OG,且EF=OG,
∴四边形EOGF为平行四边形,即EO∥FG,
又∵EO?平面BCF,FG?平面BCF,
∴EO∥平面BCF;
(Ⅱ)∵ED⊥平面ABCD,EF∥DC,
故F点到底面ABCD的距离等于ED=2,
故棱锥F-ABCD的体积为:
| 1 |
| 3 |
| 16 |
| 3 |
又∵ED⊥平面ABCD,平面ABCD为矩形,
故CD⊥平面ADE,
又由EF∥DC,
∴EF⊥平面ADE,
∴棱锥F-ADE的体积为:
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
又∵几何体ABCDEF可分割成棱锥F-ABCD和F-ADE,
故几何体ABCDEF的体积V=
| 16 |
| 3 |
| 4 |
| 3 |
| 20 |
| 3 |
点评:本题主要考查线面平行的判定方法,同时考查割补思想,以及棱锥的体积公式.

练习册系列答案
相关题目
函数y=log2
的值域为( )
| 2 |
| x2+1 |
| A、[1,+∞) |
| B、(0,1] |
| C、(-∞,1] |
| D、(-∞,1) |