题目内容
已知三点A，B，C的坐标分别为A（1，0），B（0，-1），C（cosα，sinα），其a∈（0，π）．
（1）若|
|=|
|，求角α的值．
（2）若
•
=
，求
的值．
（1）若|
| AC |
| BC |
（2）若
| AC |
| BC |
| 2 |
| 3 |
| 2sin2α+sin2α |
| 1+tanα |
考点：平面向量数量积的运算,同角三角函数基本关系的运用
专题：三角函数的求值,平面向量及应用
分析：（1）利用向量的坐标运算、向量模的几十个、同角三角函数基本关系式即可得出．
（2）利用数量积运算性质、同角三角函数基本关系式即可得出．
（2）利用数量积运算性质、同角三角函数基本关系式即可得出．
解答：
解：
=（cosα-1，sinα），
=（cosα，sinα+1）．
（1）∵|
|=|
|，
∴（cosα-1）2+sin2α=cos2α+（sinα+1）2，
∴-cosα=sinα⇒tanα=-1．
又0＜α＜π，∴α=
．
（2）
=
=2sinαcosα．
∵
•
=
，
∴cosα（cosα-1）+sinα（sinα+1）=
，
化为sinα-cosα=
，
两边平方可得：2sinαcosα=
，
∴原式=
．
| AC |
| BC |
（1）∵|
| AC |
| BC |
∴（cosα-1）2+sin2α=cos2α+（sinα+1）2，
∴-cosα=sinα⇒tanα=-1．
又0＜α＜π，∴α=
| 3π |
| 4 |
（2）
| 2sin2α+sin2α |
| 1+tanα |
| 2sinα(sinα+cosα) | ||
1+
|
∵
| AC |
| BC |
| 3 |
| 2 |
∴cosα（cosα-1）+sinα（sinα+1）=
| 3 |
| 2 |
化为sinα-cosα=
| 1 |
| 2 |
两边平方可得：2sinαcosα=
| 3 |
| 4 |
∴原式=
| 3 |
| 4 |
点评：本题考查了向量的坐标运算、向量模的几十个、同角三角函数基本关系式、数量积运算性质，考查了计算能力，属于中档题．
练习册系列答案
走进文言文系列答案
相关题目
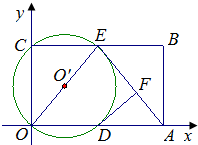如图，在平面直角坐标系中，矩形ABCO的面积为24，边OA比OC大5．E为BC的中点，以OE为直径的⊙O′交x轴于D点，过点D作DF⊥AE于点F．