题目内容
已知直线l是过点p(-1,2),直线的倾斜角为120°,圆方程ρ=2cos(θ+
);
(1)求直线l的参数方程;
(2)设直线l与圆相交于M,N两点,求|PM|•|PN|的值.
| π |
| 3 |
(1)求直线l的参数方程;
(2)设直线l与圆相交于M,N两点,求|PM|•|PN|的值.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)由于直线l是过点p(-1,2),直线的倾斜角为120°,可得直线l的参数方程为
,
化简即可得出.
(2)圆的方程ρ=2cos(θ+
)化为ρ2=2ρ(
cosθ-
sinθ),把
代入即可得出直角坐标方程.把直线l的参数方程代入可得:t2+(3+2
)t+6+2
=0.利用|PM|•|PN|=|t1t2|即可得出.
|
化简即可得出.
(2)圆的方程ρ=2cos(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
|
| 3 |
| 3 |
解答:
解:(1)∵直线l是过点p(-1,2),直线的倾斜角为120°,
∴直线l的参数方程为
,
化为
.
(2)圆的方程ρ=2cos(θ+
)化为ρ2=2ρ(
cosθ-
sinθ),
可得x2+y2=x-
y.
把直线l的参数方程代入可得:t2+(3+2
)t+6+2
=0.
∴|PM|•|PN|=|t1t2|=6+2
.
∴直线l的参数方程为
|
化为
|
(2)圆的方程ρ=2cos(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
可得x2+y2=x-
| 3 |
把直线l的参数方程代入可得:t2+(3+2
| 3 |
| 3 |
∴|PM|•|PN|=|t1t2|=6+2
| 3 |
点评:本题考查了直线的参数方程、极坐标方程化为直角坐标方程、直线参数的意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
复数z=i2(1-i)(其中i为虚数单位)的值是( )
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
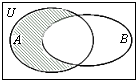
设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)<0},则图中阴影部分表示的集合为( )

| A、{x|0<x≤1} |
| B、{x|1≤x<2} |
| C、{x|x≥1} |
| D、{x|x≤1} |
函数y=(
)x+2+1(a>0,a≠1)图象必经过点( )
| 1 |
| a |
| A、(-1,1) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-2,2) |
国庆节放假,甲、乙、丙去北京旅游的概率分别是
,
,
.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|