题目内容
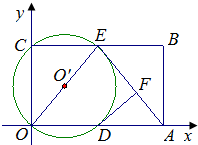如图，在平面直角坐标系中，矩形ABCO的面积为24，边OA比OC大5．E为BC的中点，以OE为直径的⊙O′交x轴于D点，过点D作DF⊥AE于点F．（1）求OA、OC的长；
（2）求证：DF为⊙O′的切线．
考点：圆的切线方程
专题：选作题,立体几何
分析：（1）根据矩形的面积公式可求得其长和宽即OA、OC的长；
（2）要证明DF为⊙O′的切线只要证明DF⊥O′D即可．
（2）要证明DF为⊙O′的切线只要证明DF⊥O′D即可．
解答：
解：（1）在矩形OABC中，设OC=x，则OA=x+5，依题意得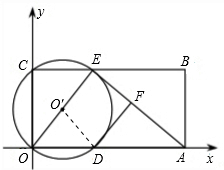
x（x+5）=24
解得x1=3，x2=-8（不合题意，舍去）
∴OC=3，OA=5．
（2）证明：连接O′D，
在矩形OABC中，OC=AB，∠OCB=∠ABC=90°，CE=BE=2.5
∴△OCE≌△ABE
∴EA=EO
∴∠EOA=∠EAO
在⊙O′中
∵O′O=O′D
∴∠O′OD=∠O′DO
∴∠O′DO=∠EAO
∴O′D∥AE
∵DF⊥AE
∴DF⊥O′D
又∵点D在⊙O′上，O′D为⊙O′的半径
∴DF为⊙O′切线．
x（x+5）=24
解得x1=3，x2=-8（不合题意，舍去）
∴OC=3，OA=5．
（2）证明：连接O′D，
在矩形OABC中，OC=AB，∠OCB=∠ABC=90°，CE=BE=2.5
∴△OCE≌△ABE
∴EA=EO
∴∠EOA=∠EAO
在⊙O′中
∵O′O=O′D
∴∠O′OD=∠O′DO
∴∠O′DO=∠EAO
∴O′D∥AE
∵DF⊥AE
∴DF⊥O′D
又∵点D在⊙O′上，O′D为⊙O′的半径
∴DF为⊙O′切线．
点评：此题考查了学生对矩形的性质，解一元二次方程及切线的性质的综合运用．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
国庆节放假，甲、乙、丙去北京旅游的概率分别是
，
，
．假定三人的行动相互之间没有影响，那么这段时间内至少有1人去北京旅游的概率为（ ）
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|