题目内容
已知函数f(x)=lnx,g(x)=x.
(1)若x>1,求证:f(x)>2g(
);
(2)是否存在实数k,使方程
g(x2)-f(1+x2)=k有四个不同的实根?若存在,求出k的取值范围;若不存在,说明理由.
(1)若x>1,求证:f(x)>2g(
| x-1 |
| x+1 |
(2)是否存在实数k,使方程
| 1 |
| 2 |
考点:根的存在性及根的个数判断,利用导数求闭区间上函数的最值
专题:计算题,证明题,导数的综合应用
分析:(1)构造函数,将不等式的证明化为函数单调性与最值的证明;(2)构造函数并求导,由数形结合求k的取值范围.
解答:
解:(1)证明:令h(x)=f(x)-2g(
)=lnx-
,x>1
h′(x)=
-
=
>0在(1,+∞)上恒成立,
∴h(x)在(1,+∞)上是增函数,
∴h(x)>h(1)=0,
∴f(x)>2g(
).
(2)设F(x)=
g(x2)-f(1+x2)=
x2-ln(1+x2),x∈R,
则F′(x)=
,
令F′(x)=0解得,x=0或x=±1,
又∵F(x)在(-∞,-1)和(0,1)上递减,在(-1,0)和(1,+∞)上递增;
且F(-1)=F(1)=
-ln2<0,F(0)=0;
∴k的取值范围是(
-ln2,0).
| x-1 |
| x+1 |
| 2x-2 |
| x+1 |
h′(x)=
| 1 |
| x |
| 4 |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
∴h(x)在(1,+∞)上是增函数,
∴h(x)>h(1)=0,
∴f(x)>2g(
| x-1 |
| x+1 |
(2)设F(x)=
| 1 |
| 2 |
| 1 |
| 2 |
则F′(x)=
| x(x+1)(x-1) |
| 1+x2 |
令F′(x)=0解得,x=0或x=±1,
又∵F(x)在(-∞,-1)和(0,1)上递减,在(-1,0)和(1,+∞)上递增;
且F(-1)=F(1)=
| 1 |
| 2 |
∴k的取值范围是(
| 1 |
| 2 |
点评:本题考查了导数的综合应用,同时考查了不等式的证明方法,属于中档题.

练习册系列答案
相关题目
函数y=(
)x+2+1(a>0,a≠1)图象必经过点( )
| 1 |
| a |
| A、(-1,1) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-2,2) |
 已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,2),且与x轴交于不同的两点A、B,点A的坐标是(1,0).
已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,2),且与x轴交于不同的两点A、B,点A的坐标是(1,0).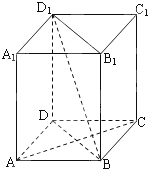 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=