题目内容
已知函数f(x)=|2x+1|+|2x-1|
(Ⅰ)求不等式f(x)≤12的解集M;
(Ⅱ)当a,b∈M时,证明:3|a+b|≤|9+ab|.
(Ⅰ)求不等式f(x)≤12的解集M;
(Ⅱ)当a,b∈M时,证明:3|a+b|≤|9+ab|.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)通过对自变量x取值范围的分类讨论,去掉原函数式中的绝对值符号,再解相应的不等式,最后取并集即可;
(Ⅱ)由(Ⅰ)知M={x|-3≤x≤3},a,b∈M,于是-3≤a≤3,-3≤b≤3,易证(9-a2)(9-b2)≥0,进一步整理可得9(a+b)2≤(9+ab)2,开方即可证得结论.
(Ⅱ)由(Ⅰ)知M={x|-3≤x≤3},a,b∈M,于是-3≤a≤3,-3≤b≤3,易证(9-a2)(9-b2)≥0,进一步整理可得9(a+b)2≤(9+ab)2,开方即可证得结论.
解答:
证明:(Ⅰ)∵f(x)=|2x+1|+|2x-1|≤12,
当x≤-
时,-(2x+1)+1-2x≤12,得x≥-3,所以-3≤x≤-
;…2分
当-
<x<
时,(2x+1)-(1-2x)≤12,2≤12成立,所以-
<x<
;.3分
当x≥
时,2x+1+2x-1≤12,解得x≤3,所以
≤x≤3;…4分
综上,M={x|-3≤x≤3}…5分
(Ⅱ)当a,b∈M时,-3≤a≤3,-3≤b≤3,…6分
a2≤9,b2≤9,9-a2≥0,9-b2≥0,(9-a2)(9-b2)≥0,…7分
即9a2+9b2≤81+a2b2,9a2++18ab+9b2≤81+18ab+a2b2,…8分
9(a+b)2≤(9+ab)2,…9分
于是有3|a+b|≤|9+ab|…10分
当x≤-
| 1 |
| 2 |
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x≥
| 1 |
| 2 |
| 1 |
| 2 |
综上,M={x|-3≤x≤3}…5分
(Ⅱ)当a,b∈M时,-3≤a≤3,-3≤b≤3,…6分
a2≤9,b2≤9,9-a2≥0,9-b2≥0,(9-a2)(9-b2)≥0,…7分
即9a2+9b2≤81+a2b2,9a2++18ab+9b2≤81+18ab+a2b2,…8分
9(a+b)2≤(9+ab)2,…9分
于是有3|a+b|≤|9+ab|…10分
点评:本题考查不等式的证明,着重考查分类讨论思想与等价转化思想的综合运用,考查推理论证能力,属于难题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
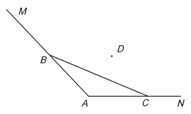 在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.