题目内容
8.已知直线l:x-2y+m=0,A(1,1),B(2,3),C(3,t).(1)求过点B且与l垂直的直线的方程;
(2)若直线l过点A,且与线段BC有交点,求t的范围.
分析 (1)求出直线l的斜率,从而求出与l垂直的直线的斜率,根据点斜式方程求出即可;(2)将A(1,1)代入直线l,求出m的值,结合图象求出t的范围即可.
解答 解:(1)直线l的斜率是:$\frac{1}{2}$,
故所求直线的斜率是-2,
过B(2,3),斜率是-2的直线方程是:
y-3=-2(x-2),
整理得:2x+y-7=0;
(2)将A(1,1)代入直线l得:
1-2+m=0,解得:m=1,
直线l:x-2y+1=0,
如图示: ,
,
将x=3代入直线l得:
3-2y+1=0,解得:y=2,
故只需t≤2即可.
点评 不同考查了求直线方程问题,考查数形结合思想,是一道中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )
| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
19.设随机变量X服从正态分布N(2,22),则P(2<X<3)可以表示为( )
| A. | 1~P(X<1) | B. | $\frac{1-2P(X<1)}{2}$ | C. | P(0<X<1) | D. | $\frac{1+2P(X<1)}{2}$ |
16.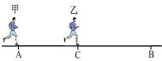 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )| A. | x1+x2 | B. | $\frac{({x}_{1}+{x}_{2})^{2}}{4{x}_{1}}$ | ||
| C. | $\frac{{x}_{1}^{2}}{4({x}_{1}+{x}_{2})}$ | D. | $\frac{({x}_{1}+{x}_{2})^{2}}{({x}_{1}-{x}_{2}){x}_{1}}$ |
10.已知正数a,b满足ab≥a+b+8则a+b的最小值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |