题目内容
17．等比数列{an}的公比q=-$\frac{1}{3}$，前4项的和为$\frac{5}{9}$，则a1=$\frac{3}{4}$．分析 直接利用等比数列的前n项和公式列式求得a1．
解答 解：在等比数列{an}中，由q=-$\frac{1}{3}$，S4=$\frac{5}{9}$，
得${S}_{4}=\frac{{a}_{1}（1-{q}^{4}）}{1-q}=\frac{{a}_{1}[1-（-\frac{1}{3}）^{4}]}{1+\frac{1}{3}}=\frac{5}{9}$，
即$\frac{80}{81}{a}_{1}=\frac{20}{27}$，解得${a}_{1}=\frac{3}{4}$．
故答案为：$\frac{3}{4}$．
点评 本题考查等比数列的前n项和，是基础的计算题．
练习册系列答案
相关题目
7．
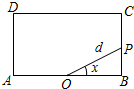如图，已知矩形ABCD中，AB=2，BC=1，O为线段AB的中点，动点P从B出发，沿矩形ABCD的边逆时针运动，运动至A点时终止．设∠BOP=x，OP=d，将d表示为x的函数d=f（x）．则下列命题中：
①f（x）有最小值1；
②f（x）有最大值$\sqrt{2}$；
③f（x）有3个极值点；
④f（x）有4个单调区间．
其中正确的是（ ）
如图，已知矩形ABCD中，AB=2，BC=1，O为线段AB的中点，动点P从B出发，沿矩形ABCD的边逆时针运动，运动至A点时终止．设∠BOP=x，OP=d，将d表示为x的函数d=f（x）．则下列命题中：①f（x）有最小值1；
②f（x）有最大值$\sqrt{2}$；
③f（x）有3个极值点；
④f（x）有4个单调区间．
其中正确的是（ ）
| A． | ①② | B． | ②③ | C． | ①②④ | D． | ①②③④ |
12．在△ABC中，$\overrightarrow{AP}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），若（sinC）•$\overrightarrow{AC}$+（sinA）•$\overrightarrow{PA}$+（sinB）•$\overrightarrow{PB}$=$\overrightarrow{0}$，则△ABC的形状为（ ）
| A． | 等边三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
6．《九章算术》有这样一个问题：今有男子善走，日增等里，九日走一千二百六十里，第一日、第四日、第七日所走之和为三百九十里，问第八日所走里数为（ ）
| A． | 150 | B． | 160 | C． | 170 | D． | 180 |
19．如果椭圆的长轴长为4，短轴长为2，则此椭圆的标准方程为（ ）
| A． | $\frac{x^2}{4}+{y^2}$=1 | B． | $\frac{y^2}{4}+{x^2}$=1 | ||
| C． | $\frac{x^2}{4}+{y^2}$=1或$\frac{y^2}{4}+{x^2}$=1 | D． | $\frac{y^2}{4}+\frac{x^2}{2}$=1 |