题目内容
13.已知圆C1:(x-2)2+(y-3)2=1.圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则PM+PN的最小值为5$\sqrt{2}$-4.分析 根据题意画出图形,结合图形,求出圆C1关于x轴的对称圆的圆心坐标A与半径,再求出圆A与圆C2的圆心距减去两个圆的半径和,即为|PM|+|PN|的最小值.
解答 解:如图所示,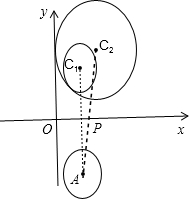
圆C1关于x轴的对称圆的圆心坐标A(2,-3),半径为1,
圆C2的圆心坐标C2(3,4),半径为3,
|PM|+|PN|的最小值为圆A与圆C2的圆心距减去两个圆的半径和,
即为$\sqrt{{(3-2)}^{2}{+(4+3)}^{2}}$-4=5$\sqrt{2}$-4.
故答案为:5$\sqrt{2}$-4.
点评 本题考查圆的对称圆方程以及两圆的位置关系,两点距离公式的应用问题,也考查了转化思想与计算能力,数形结合思想的应用问题,是综合性题目.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
4.已知等差数列{an}的前n项和为Sn,a2=-2,a8=6,则S9=( )
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |