题目内容
16.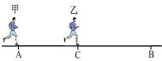 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )| A. | x1+x2 | B. | $\frac{({x}_{1}+{x}_{2})^{2}}{4{x}_{1}}$ | ||
| C. | $\frac{{x}_{1}^{2}}{4({x}_{1}+{x}_{2})}$ | D. | $\frac{({x}_{1}+{x}_{2})^{2}}{({x}_{1}-{x}_{2}){x}_{1}}$ |
分析 设AB两地距离为S,则乙从C到B时间为t,对乙:S-S2=$\frac{1}{2}a{t}^{2}$,当甲通过S1所用时间为t1,则:S1=$\frac{1}{2}a{{t}_{1}}^{2}$,设甲从A到B的总时间为t2,则S=$\frac{1}{2}a{{t}_{2}}^{2}$,由此结合题意能求出结果.
解答 解:设AB两地距离为S,则乙从C到B时间为t,
对乙:S-S2=$\frac{1}{2}a{t}^{2}$,
当甲通过S1所用时间为t1,则:S1=$\frac{1}{2}a{{t}_{1}}^{2}$,
设甲从A到B的总时间为t2,则S=$\frac{1}{2}a{{t}_{2}}^{2}$,
根据题意可以得到:
t2-t1=t,整理可以到的:S=$\frac{({S}_{1}+{S}_{2})^{2}}{4{S}_{1}}$,
故选项B正确,选项ACD错误.
故选:B.
点评 本题考查匀变速直线规律的应用,注意利用时间相等列出方程式即可求解,是中档题.

练习册系列答案
相关题目
7.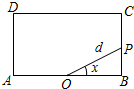 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
①f(x)有最小值1;
②f(x)有最大值$\sqrt{2}$;
③f(x)有3个极值点;
④f(x)有4个单调区间.
其中正确的是( )
 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:①f(x)有最小值1;
②f(x)有最大值$\sqrt{2}$;
③f(x)有3个极值点;
④f(x)有4个单调区间.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ①②④ | D. | ①②③④ |
4.已知等差数列{an}的前n项和为Sn,a2=-2,a8=6,则S9=( )
| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
11.方程组$\left\{\begin{array}{l}{ax-y=0}\\{x-(2a-1)y=1}\end{array}\right.$有且只有一个解,则a的取值范围为( )
| A. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞) | B. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,+∞) | ||
| C. | (-∞,1)∪(1,+∞) | D. | R |
6.《九章算术》有这样一个问题:今有男子善走,日增等里,九日走一千二百六十里,第一日、第四日、第七日所走之和为三百九十里,问第八日所走里数为( )
| A. | 150 | B. | 160 | C. | 170 | D. | 180 |