题目内容
过点（2，
）且平行于极轴的直线的坐标方程为（ ）
| π |
| 3 |
A、ρsinθ=
| ||
B、ρcosθ=
| ||
| C、ρsinθ=2 | ||
| D、ρcosθ=2 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：由点（2，
）可得直角坐标(1，
)．设P（ρ，θ）为所求直线上的任意一点，则ρ=
，即可得出．
| π |
| 3 |
| 3 |
| ||
| sinθ |
解答：
解：由点（2，
）可得直角坐标为(2cos
，2sin
)，即(1，
)．
设P（ρ，θ）为所求直线上的任意一点，
则ρ=
，即ρsinθ=
．
故选：A．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
设P（ρ，θ）为所求直线上的任意一点，
则ρ=
| ||
| sinθ |
| 3 |
故选：A．
点评：本题考查了直线的极坐标方程、极坐标与直角坐标的互化，考查了计算能力，属于基础题．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
已知三棱锥的三视图，则该三棱锥的体积是（ ）
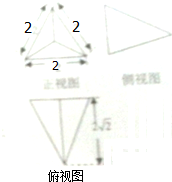
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆的方程为（x-t）2+（y-t-1）2=2（t∈[-2，2]），则它的圆心的轨迹方程为（ ）
| A、x-y+1=0，x∈[-2，2] |
| B、x+y+1=0，x∈[-2，2] |
| C、x-y-1=0，x∈[-2，2] |
| D、x+y-1=0，x∈[-2，2] |
平面直角坐标系中，O为坐标原点，动点B，C分别在x轴和y轴上，且BC=2
，设过O，B，C三点的动圆扫过的区域边界所代表的曲线为C．已知P是直线l：3x-4y+20=0上的动点，PM，PN是曲线C的两条切线，M，N为切点，那么四边形PMON面积的最小值是（ ）
| 2 |
| A、20 | B、16 | C、12 | D、8 |
若22a+1＞(
)1-a成立，则a的取值范围为（ ）
| 1 |
| 2 |
| A、（-1，+∞） |
| B、（-2，+∞） |
| C、（-1，0） |
| D、（-∞，-2） |